如图，在平面直角坐标系中，抛物线y=-x2+bx+c（a≠0）经过A、B、C三点，点A、C的坐标分别是（0，4）、（-1，0）．（1）求此抛物线的解析式；（2）点P是第一象限内抛物线上的一动点，当△ABP

Question

如图，在平面直角坐标系中，抛物线y=-x²+bx+c（a≠0）经过A、B、C三点，点A、C的坐标分别是（0，4）、（-1，0）．
（1）求此抛物线的解析式；
（2）点P是第一象限内抛物线上的一动点，当△ABP的面积最大时，求出此时P的坐标及面积的最大值；
（3）若G为抛物线上的一动点，F为x轴上的一动点，点D坐标为（1，4），点E坐标为（1，0），当D、E、F、G构成平行四边形时，请直接写出点G的坐标．

Answer 1

（1）将A，C点坐标代入函数解析式，得

-1-b+c=0

c=4

，
解得

b=3

c=4

，
抛物线的解析式为y=-x²+3x+4；
（2）作PE⊥x轴交AB于E点，如图1，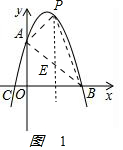
当y=0时，-x²+3x+4=0，解得x₁=-1（不符合题意，舍），x₂=4，即B点坐标为（4，0），
AB的解析式为y=kx+b，将A，B点坐标代入函数解析式，得
y=-x+4．
设P点坐标为（m，-m²+3m+4），E（m，-m+4），
PE=-m²+3m+4-（-m+4）=-m²+4m，
S_△ABP=(1)/(2)AB•x_B=(1)/(2)（-m²+4m）×4=-2（m-2）²+8，
当m=2时，S_△ABP有最大值，最大值是8，
m=2，-m²+3m+4=-4+6+4=6，即P点坐标为（2，6）；
（3）如图2，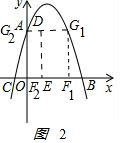
由四边形DEFG是平行四边形，E，F在x轴上，得
GF=DE=4，
当y=4时，-x²+3x+4=4，解得x₁=0，x₂=3，即D点坐标为（0，4）或（3，4）．
当D、E、F、G构成平行四边形时，点G的坐标（0，4）或（3，4）．