早教吧作业答案频道 -->数学-->
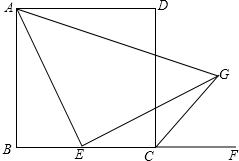
如图,E为正方形ABCD的边BC上一点,CG平分∠DCF,连接AE,过点E作EG⊥AE交CG于点G.求证:AE=EG.
题目详情
如图,E为正方形ABCD的边BC上一点,CG平分∠DCF,连接AE,过点E作EG⊥AE交CG于点G.求证:AE=EG.

▼优质解答
答案和解析
证明:在AB上截取BM=BE,
∵四边形ABCD是正方形,
∴AB=BC,∠B=∠BCD=∠DCF=90°,
∴AM=CE,
∴∠BME=∠BEM=45°,
∴∠AME=135°,
∵CG平分∠DCF,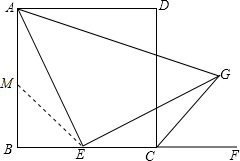
∴∠GCF=45°,
∴∠ECG=135°,
∴∠AME=∠ECG,
∵EG⊥AE,
∴∠AEB+∠CEG=90°,
又∵∠MAE+∠AEB=90°,
∴∠MAE=∠CEG,
在△AME和△ECG中,
,
∴△AME≌△ECG(ASA),
∴AE=EG.
∵四边形ABCD是正方形,
∴AB=BC,∠B=∠BCD=∠DCF=90°,
∴AM=CE,
∴∠BME=∠BEM=45°,
∴∠AME=135°,
∵CG平分∠DCF,

∴∠GCF=45°,
∴∠ECG=135°,
∴∠AME=∠ECG,
∵EG⊥AE,
∴∠AEB+∠CEG=90°,
又∵∠MAE+∠AEB=90°,
∴∠MAE=∠CEG,
在△AME和△ECG中,
|
∴△AME≌△ECG(ASA),
∴AE=EG.
看了如图,E为正方形ABCD的边B...的网友还看了以下:
平衡转化率(2)若反应物不止一种时,如A(g)+B(g)=C(g)+D(g)①若只增加A的量,平衡 2020-05-16 …
已知A(g)+B(g)=C(g)△H=△H1D(g)+B(g)=E(g)△H=△H2,若A和D混合 2020-05-20 …
在等温等容的条件下,化学反应方程式为:A(g)+B(g)=C(g),充入一定量A,A和B的转化率怎 2020-06-06 …
平衡转化率,为什么?若反应物不止一种时,如A(g)+B(g)=C(g)+D(g)①若只增加A的量, 2020-06-15 …
同等程度地改变反应混合物中各物质的浓度时,应视为压强的影响这句话什么意思A(g)+B(g)=C(g 2020-06-22 …
反应A(g)+B(g)—→C(g)ΔH,分两步进行:①A(g)+B(g)—→X(g)ΔH1;②X(g 2020-10-31 …
反应A(g)+B(g)―→C(g)ΔH,分两步进行:①A(g)+B(g)―→X(g)ΔH1;②X(g 2020-10-31 …
反应A(g)+B(g)―→C(g)ΔH,分两步进行:①A(g)+B(g)―→X(g)ΔH1②X(g) 2020-10-31 …
对于反应A(g)+B(g)C(g)+D(g)在密闭容器里已达到平衡此时向容器内充入A气体,使其浓度增 2020-11-03 …
可逆反应A(s)=B(g)+C(g)平衡常数K=c(B)*c(C),保持温度不变缩小容器体积,重新平 2020-12-05 …