早教吧作业答案频道 -->数学-->
如图,平行四边形ABCD中,AD=9cm,CD=32cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)(1)求BC边上高AE的长度;(2)连接AN、CM,当t
题目详情
如图,平行四边形ABCD中,AD=9cm,CD=3
cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)
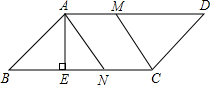
(1)求BC边上高AE的长度;
(2)连接AN、CM,当t为何值时,四边形AMCN为菱形;
(3)作MP⊥BC于P,NQ⊥AD于Q,当t为何值时,四边形MPNQ为正方形.
| 2 |

(1)求BC边上高AE的长度;
(2)连接AN、CM,当t为何值时,四边形AMCN为菱形;
(3)作MP⊥BC于P,NQ⊥AD于Q,当t为何值时,四边形MPNQ为正方形.
▼优质解答
答案和解析
(1)∵四边形ABCD是平行四边形,
∴AB=CD=3
cm.
在直角△ABE中,∵∠AEB=90°,∠B=45°,
∴AE=AB•sin∠B=3
×
=3(cm);
(2)∵点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6),
∴AM=CN=t,
∵AM∥CN,
∴四边形AMCN为平行四边形,
∴当AN=AM时,四边形AMCN为菱形.
∵BE=AE=3,EN=6-t,
∴AN2=32+(6-t)2,
∴32+(6-t)2=t2,
解得t=
.
 故当t为
故当t为
时,四边形AMCN为菱形;
(3)∵MP⊥BC于P,NQ⊥AD于Q,QM∥NP,
∴四边形MPNQ为矩形,
∴当QM=QN时,四边形MPNQ为正方形.
∵AM=CN=t,BE=3,
∴AQ=EN=BC-BE-CN=9-3-t=6-t,
∴QM=AM-AQ=t-(6-t)=2t-6,
∵QN=AE=3,
∴2t-6=3,
解得t=4.5.
故当t为4.5时,四边形MPNQ为正方形.
∴AB=CD=3
| 2 |
在直角△ABE中,∵∠AEB=90°,∠B=45°,
∴AE=AB•sin∠B=3
| 2 |
| ||
| 2 |
(2)∵点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6),
∴AM=CN=t,
∵AM∥CN,
∴四边形AMCN为平行四边形,
∴当AN=AM时,四边形AMCN为菱形.
∵BE=AE=3,EN=6-t,
∴AN2=32+(6-t)2,
∴32+(6-t)2=t2,
解得t=
| 15 |
| 4 |
 故当t为
故当t为| 15 |
| 4 |
(3)∵MP⊥BC于P,NQ⊥AD于Q,QM∥NP,
∴四边形MPNQ为矩形,
∴当QM=QN时,四边形MPNQ为正方形.
∵AM=CN=t,BE=3,
∴AQ=EN=BC-BE-CN=9-3-t=6-t,
∴QM=AM-AQ=t-(6-t)=2t-6,
∵QN=AE=3,
∴2t-6=3,
解得t=4.5.
故当t为4.5时,四边形MPNQ为正方形.
看了如图,平行四边形ABCD中,A...的网友还看了以下:
求(1+x+1/x平方)的10次方展开试中的常数我是怎样算的。T(r+1)=C(10,r)*(1+ 2020-05-13 …
matlab 结果用参数表示syms t a b c h;u=a/(4*3*2*1)*t^4+b/ 2020-05-16 …
我国目前现货交易实行的是()交易模式A.“T+1”或“T+0”B.“T+0”C.“T+1”D.“T+ 2020-05-22 …
您好,我想问下T(r+1)=C(r,n)a^nb^(n-r)这个公式,为什么第N项写成r+1的形式 2020-06-11 …
T日的基金份额净值在当天收市后计算,并在( )日公告。A.TB.T+1 C.T+2D.T+3 2020-06-27 …
什么是二项式的通式?在二项式定理(a+b)^n=C(n,0)a^n+C(n,1)a^(n-1)b+ 2020-07-31 …
利用行列式性质证明等式=0:第一行1,a,b,c+d第二行1,b,c,a+d第三行1,c,d,a+b 2020-11-24 …
如图,四边形AOBC为直角梯形,OC=根号5,OB=5AC,OC所在的直线的解析式为y=2x,平行于 2020-12-05 …
x=t^2dx=2tdt∫﹙√x﹚^3+1/√x+1dx=2∫{[t³+1]/[t+1]}tdt=2 2020-12-17 …
下图是北京城郊年平均气温分布图。北京前门与通州相比.年平均气温的差值T最大可达[]A.1.8℃<T< 2021-01-10 …