某校为美化校园，准备在长32m，宽20m的长方形场地上修建宽度相等的一条东西方向、两条南北方向的长方形花廊，余下部分作为活动场所，要求余下的活动场所总面积为442m2，甲、乙两种设

Question

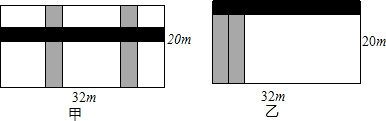
某校为美化校园，准备在长32m，宽20m的长方形场地上修建宽度相等的一条东西方向、两条南北方向的长方形花廊，余下部分作为活动场所，要求余下的活动场所总面积为442m²，甲、乙两种设计方案如图所示．
（1）分别求出这两种方案中花圃的宽度．
（2）比较你所列的两个方程，方案甲可以转化为方案乙求解吗？为什么？

Answer 1

（1）设甲设计方案中花圃的宽为xm，由题意得：
（32-2x）（20-x）=442，
解得：x₁=3，x₂=33（不合题意舍去），
20-3=17（米），
答：甲设计方案中花圃的宽为17m；
设乙设计方案中花圃的宽为ym，由题意得：
（32-2y）（20-y）=442，
解得：y₁=3，y₂=33（不合题意舍去），
20-3=17（米），
答：乙设计方案中花圃的宽为17m；

（2）方案甲可以转化为方案乙求解，利用平移方法可以把小路平移到长方形场地的两个边上，然后表示花圃的宽和长，根据面积是442m²可得方程．