早教吧作业答案频道 -->数学-->
如图,BC=2,A为半径为1的⊙B上一点,连接AC,在AC上方作一个正六边形ACDEFG,连接BD,则BD的最大值为.
题目详情
如图,BC=2,A为半径为1的⊙B上一点,连接AC,在AC上方作一个正六边形ACDEFG,连接BD,则BD的最大值为___.
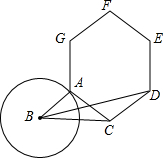

▼优质解答
答案和解析
∵六边形ACDEFG是正六边形,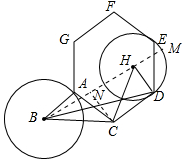
∴AC=CD,∠ACD=(6-2)×180°÷6=120°,
把△ABC和⊙B绕点C旋转120°得△DHC和⊙H,BH的延长线与⊙H的交点为M,
作CN⊥BM于N,如图所示:
则BM的长度就是DB达到的最大值,∠BCH=120°,CH=CB=2,BN=HN,
∴∠B=∠CHB=(180°-120°)÷2=30°,
∴CN=
BC=1,
∴BN=
=
,
∴BH=2BN=2
,
∴BM=BH+HM=2
+1,
即BD的最大值为2
+1,
故答案为:2
+1.

∴AC=CD,∠ACD=(6-2)×180°÷6=120°,
把△ABC和⊙B绕点C旋转120°得△DHC和⊙H,BH的延长线与⊙H的交点为M,
作CN⊥BM于N,如图所示:
则BM的长度就是DB达到的最大值,∠BCH=120°,CH=CB=2,BN=HN,
∴∠B=∠CHB=(180°-120°)÷2=30°,
∴CN=
| 1 |
| 2 |
∴BN=
| BC2-CN2 |
| 3 |
∴BH=2BN=2
| 3 |
∴BM=BH+HM=2
| 3 |
即BD的最大值为2
| 3 |
故答案为:2
| 3 |
看了如图,BC=2,A为半径为1的...的网友还看了以下:
已知二次函数y=x^2-(p-2)x-4+p1.证明:无论p取什么实数值,这个函数的图像与x轴总有 2020-05-13 …
1.比如一个三次函数其本身图像又两个极值点(对应有极值)与x轴有三个交点,但是导函数图像(二次函数 2020-05-17 …
1.如果AB=2AM那么M是线段AB的中点2.如果M是AB内的一点并且MA=MB那么点M是线段AB 2020-05-22 …
1.如果MA=MB那么点M是线段AB的中点2.如果MA=AB那么点M是线段AB的中点这两句话对吗? 2020-05-22 …
1,.如图1,已知△ABC是等边三角形,BD是高,延长BC到点E,使CE=CD,过点D作DF⊥BE 2020-06-03 …
如图正方体ABCD-A1B1C1D1中,EF分别是AB和AA1的中点,求证E,C,D1,F四面共点 2020-07-09 …
判断题:如果每一个有理数都是一个集合S的极限点,那么每一个无理数也是这个S的极限点1.如果每一个有 2020-07-30 …
关于平面直角坐标的数学问题1.如果一些点在平行于x轴的直线上,那么这些点的纵坐标有什么特点?2.如 2020-08-01 …
小刚同学自己设计了一个有“高”、“中”、“低”三档火力的电火锅,其电路图如图所示,现在要使电火锅调到 2020-11-30 …
小宇同学自己设计了一个有“高”、“中”、“低”三档火力的电火锅,其电路如图所示,现在要使火锅调到“高 2020-11-30 …