如图所示，水平面上的圆柱形容器中分别盛有A、B两种不同液体，且A、B液体对各自容器底部的压力相等．现在量容器中分别放入甲、乙两个物体后（液体不溢出），两液体对容器底部的压强

Question

如图所示，水平面上的圆柱形容器中分别盛有A、B两种不同液体，且A、B液体对各自容器底部的压力相等．现在量容器中分别放入甲、乙两个物体后（液体不溢出），两液体对容器底部的压强相等，下列说法中正确的是（　　）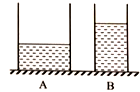

A. 若甲、乙都漂浮，则可能m_甲=m_乙

B. 若甲、乙都漂浮，则可能V_甲<V_乙

C. 若甲、乙都浸没，则一定m_甲<m_乙

D. 若甲、乙都浸没，则一定V_甲>V_乙

Answer 1

由于在水平面上容器是圆柱形容器，对于柱形容器，液体对容器底的压力等于液体的重力；则已知A、B液体对各自容器底部的压力相等，所以A、B液体重力相等，即G_A=G_B；
A和B、若甲、乙都漂浮，根据漂浮条件可知：F_甲浮=G_甲，F_乙浮=G_乙；
由于此时两液体对容器底部的压强相等，即：p_A′=p_B′，
则根据F=pS可知液体对容器底的压力：
F_A′=p_A′S_A，F_B′=p_B′S_B，
由图可知：S_A>S_B；则F_A′>F_B′，
由于柱形容器中甲、乙都漂浮，液体对容器底的压力等于液体的重力和物体的重力之和；
则F_A′=G_A+G_甲；F_B′=G_B+G_乙；
所以，G_甲>G_乙，则根据m=(G)/(g)可知：m_甲>m_乙，故A错误；
由于甲、乙两个物体的密度未知，所以物体的体积大小关系不能判断，可能V_甲<V_乙，故B正确；
C和D、若甲、乙都浸没，
由图可知S_A>S_B；根据A、B液体对各自容器底部的压力相等，
因为此时两液体对容器底部的压强相等，即：p_A′=p_B′，
根据F=pS可知：此时两液体对容器底部的压力关系是：F_A′>F_B′，
则液体对容器底部的压力变化量为，△F_A>△F_B；
由于甲、乙都处于浸没，则△F=G_排，G≥G_排，
所以，G_甲≥△F_A′>△F_B′，G_乙≥△F_B′，
则根据m=(G)/(g)可知：m_甲与m_B的大小关系都有可能，故C错误；
A、B液体对各自容器底部的压力相等，利用p=(F)/(S)和p=ρgh可知：
ρ_Ah_AS_A=ρ_Bh_BS_B；
两液体对容器底部的压强相等时，根据p=ρgh可知：ρ_Ah_A′=ρ_Bh_B′，
由图可知S_A>S_B；
ρ_Ah_A′S_A>ρ_Bh_B′S_B；
由于△h=h′-h，所以，S_A△h_A>S_Bρ_B△h_B；
由于甲、乙物体浸没，则体积分别为V_甲=S_A△h_A，V_乙=S_B△h_B，
V_甲ρ_A>V_乙ρ_B；
则(V甲)/(V乙)>(ρB)/(ρA)，
由于两液体的密度无法判断，所以V_甲与V_乙的大小不能都有可能，故D错误．
故选B．