早教吧作业答案频道 -->数学-->
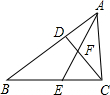
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的角平分线,AE与CD交于点F,求证:△CEF是等腰三角形.
题目详情
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的角平分线,AE与CD交于点F,求证:△CEF是等腰三角形.

▼优质解答
答案和解析
证明:∵在△ABC中,∠ACB=90°,
∴∠B+∠BAC=90°,
∵CD是AB边上的高,
∴∠ACD+∠BAC=90°,
∴∠B=∠ACD,
∵AE是∠BAC的角平分线,
∴∠BAE=∠EAC,
∴∠B+∠BAE=∠ACD+∠EAC,
即∠CEF=∠CFE,
∴CE=CF,
∴△CEF是等腰三角形.
∴∠B+∠BAC=90°,
∵CD是AB边上的高,
∴∠ACD+∠BAC=90°,
∴∠B=∠ACD,
∵AE是∠BAC的角平分线,
∴∠BAE=∠EAC,
∴∠B+∠BAE=∠ACD+∠EAC,
即∠CEF=∠CFE,
∴CE=CF,
∴△CEF是等腰三角形.
看了 如图,在△ABC中,∠ACB...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
matlab解中学三角函数方程数学题,不会求大大~~~~~~~~~~[a,b,c,A,B,C]=s 2020-05-14 …
1、已知a,b,c互不相等求2a-b-c/(a-b)(b-c)+2b-c-a/(b-c)(b-a) 2020-05-16 …
分解因式(a-b-c)(a+b-c)-(b-c-a)(b+c-a)正确答案是这个:(a+b-c)( 2020-05-17 …
已知a+b+c=0,试求a^2/(2a^2+bc)+b^2/(2b^2+ac)+c^2/(2c^2 2020-06-11 …
a(b-c)^5+b(c-a)^5+c(a-b)^5分解为(a-b)(b-c)(c-a)L(aa( 2020-07-09 …
利用(a+b+c)^2=a^2+b^2^c^2+2ab+2ac+abc,推导(a+b+c)^2+a 2020-07-30 …
(a+b+c)^3-(b+c-a)^3-(c+a-b)^3-(a+b-c)^3=[(a+b+c)^ 2020-08-02 …
已知a、b、c满足a<b<c,ab+bc+ac=0,abc=1,则()A.|a+b|>|c|B.|a 2020-11-01 …
判断下列命题的真假已知a,b,c,d∈R(1)若ac>bc,则a>b(2)若a>-b,则c-ab>c 2020-12-13 …