竖直平面内有一半径为r、电阻为R1、粗细均匀的光滑半圆形金属环，在M、N处与距离为2r、电阻不计的平行光滑金属导轨ME、NF相接，E、F之间接有电阻R2，已知R1=12R，R2=4R．在MN上方及CD下方有

Question

竖直平面内有一半径为r、电阻为R₁、粗细均匀的光滑半圆形金属环，在M、N处与距离为2r、电阻不计的平行光滑金属导轨ME、NF相接，E、F之间接有电阻R₂，已知R₁=12R，R₂=4R．在MN上方及CD下方有水平方向的匀强磁场Ⅰ和Ⅱ，磁感应强度大小均为B．现有质量为m、电阻不计的导体棒ab，从下图中半圆环的最高点A处由静止下落，在下落过程中导体棒始终保持水平，与半圆形金属环及轨道接触良好，设平行导轨足够长．已知导体棒下落r/2时的速度大小为v₁，下落到MN处时的速度大小为v₂．求：

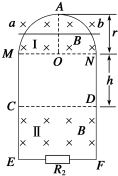
（1）求导体棒ab从A处下落到MN和CD之间的加速度大小；
（2）若导体棒ab进入磁场Ⅱ后棒中电流大小始终不变，求磁场Ⅰ和Ⅱ之间的距离h和R₂上的电功率P₂；
（3）当CD边界在某一位置时，导体棒ab进入磁场恰好能做匀速直线运动．若再将磁场Ⅱ的CD边界略微下移，已知此时导体棒ab刚进入磁场Ⅱ时的速度大小为v₃，要使其在外力F作用下做匀加速直线运动，加速度大小为a，求所加外力F随时间变化的关系式．

Answer 1

（1）导体棒ab从A处下落到MN和CD之间时只受重力作用，
由牛顿第二定律有：mg=ma
解得：a=g；
（2）当导体棒ab通过磁场Ⅱ时，棒中电流大小始终不变，则需要安培力恰好等于重力，则有：
mg=BI•2r                     
又由于I=(B•2r•vt)/(R并)
解得R_并=(12R×4R)/(12R+4R)=3R
v_t=(3mgR)/(4B2r2)；
导体棒从MN到CD做加速度为g的匀加速直线运动，则有
v_t²-v₂²=2gh，
解得：h=(9m2gR2)/(32B4r4)-(v22)/(2g)，
又IR2=(B•2r•vt)/(4R)             
R₂上的电功率：P2=

I

2 R2

R2
解得：P₂=(9m2g2R)/(16B2r2)；
（3）设导体棒ab进入磁场Ⅱ后经过时间t的速度大小为v_t′，此时安培力大小为
F′=(4B2r2vt′)/(3R)                
由于导体棒ab做匀加速直线运动，则有
v_t′=v₃+at  
根据牛顿第二定律有：
F+mg-F′=ma  
解得：F=(4B2r2a)/(3R)t+(4B2r2v3)/(3R)+ma-mg．
答：（1）导体棒ab从A处下落到MN和CD之间的加速度大小为g；
（2）若导体棒ab进入磁场Ⅱ后棒中电流大小始终不变，磁场Ⅰ和Ⅱ之间的距离为(9m2gR2)/(32B4r4)-(v22)/(2g)，R₂上的电功率(9m2g2R)/(16B2r2)；
（3）所加外力F随时间变化的关系式为F=(4B2r2a)/(3R)t+