早教吧作业答案频道 -->数学-->
感知:如图①,在△ABC中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°,求∠DAE度数;探究:如图②,在△ABC中,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC,其他条件不变,求∠DFE的度数”
题目详情
感知:如图①,在△ABC中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°,求∠DAE度数;
探究:如图②,在△ABC中,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC,其他条件不变,求∠DFE的度数”;
拓展:如图③,若把△ABC变成四边形ABEC,把AE⊥BC变成EA平分∠BEC,其他条件不变,∠DAE的度数是否变化,并且说明理由.
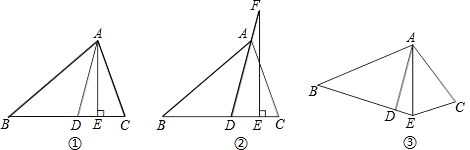
探究:如图②,在△ABC中,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC,其他条件不变,求∠DFE的度数”;
拓展:如图③,若把△ABC变成四边形ABEC,把AE⊥BC变成EA平分∠BEC,其他条件不变,∠DAE的度数是否变化,并且说明理由.

▼优质解答
答案和解析
(1)∵∠B=40°,∠C=70°,
∴∠BAC=70°,
∵AD平分∠BAC,
∴∠BAD=∠CAD=35°,
∴∠ADE=∠B+∠BAD=75°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠DAE=90°-∠ADE=15°.
(2)同(1),可得,∠ADE=75°,
∵FE⊥BC,
∴∠FEB=90°,
∴∠DFE=90°-∠ADE=15°.
(3)结论:∠DAE的度数大小不变.
证明:∵AE平分∠BEC,
∴∠AEB=∠AEC,
∴∠C+∠CAE=∠B+∠BAE,
∵∠CAE=∠CAD-∠DAE,∠BAE=∠BAD+∠DAE,
∴∠C+∠CAD-∠DAE=∠B+∠BAD+∠DAE,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴2∠DAE=∠C-∠B=30°,
∴∠DAE=15°.
∴∠BAC=70°,
∵AD平分∠BAC,
∴∠BAD=∠CAD=35°,
∴∠ADE=∠B+∠BAD=75°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠DAE=90°-∠ADE=15°.
(2)同(1),可得,∠ADE=75°,
∵FE⊥BC,
∴∠FEB=90°,
∴∠DFE=90°-∠ADE=15°.
(3)结论:∠DAE的度数大小不变.
证明:∵AE平分∠BEC,
∴∠AEB=∠AEC,
∴∠C+∠CAE=∠B+∠BAE,
∵∠CAE=∠CAD-∠DAE,∠BAE=∠BAD+∠DAE,
∴∠C+∠CAD-∠DAE=∠B+∠BAD+∠DAE,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴2∠DAE=∠C-∠B=30°,
∴∠DAE=15°.
看了感知:如图①,在△ABC中,A...的网友还看了以下:
图中构成东西半球分界线的两条经线是()A.A线和C线B.A线和D线C.B线和C线D.B线和D线 2020-04-23 …
图中构成东西半球分界线的两条经线是()A.A线和C线B.A线和D线C.B线和C线D.B线和D线 2020-04-23 …
读世界海陆分布图,回答5~6题图中构成东西半球分界线的经线是()A.A线和C线B.A线和D线C.B 2020-04-23 …
图中构成东西半球分界线的两条经线是()A.A线和C线B.A线和D线C.B线和C线D.B线和D线 2020-04-23 …
15.图中构成东西半球分界线的两条经线是()A.A线和C线B.A线和D线C.B线和C线D.B线和D 2020-04-23 …
图中构成东西半球分界线的两条经线是()A.A线和C线B.A线和D线C.B线和C线D.B线和D线 2020-04-23 …
读世界七大洲分布图,回答4-7题.图中构成东西半球分界线的两条经线是()A.A线和C线B.A线和D 2020-04-23 …
图中构成东西半球分界线的两条经线是()A、a线和c线B、a线和d线C、b线和c线D、b线和d线 2020-04-23 …
小明还想看看东半球的主要国家,他应看的范围是()A.A线和C线之间B.A线和D线之间C.B线和C线 2020-05-13 …
小明还想看看东半球的主要国家,他应看的范围是()A、A线和C线之间B、A线和D线之间C、B线和C线 2020-05-13 …