早教吧作业答案频道 -->数学-->
我们已经知道(a+b)2=a2+2ab+b2,(a+b)n(n为非负整数)的计算结果有什么规律呢?实际上我国宋代就有数学家进行了研究:如果将(a+b)n(n为非负整数)的每一项按字母a的次数由大到小排
题目详情
我们已经知道(a+b)2=a2+2ab+b2,(a+b)n(n为非负整数)的计算结果有什么规律呢?实际上我国宋代就有数学家进行了研究:
如果将(a+b)n(n为非负整数)的每一项按字母a的次数由大到小排列,就可以得到下面的等式:
(a+b)0=1,它只有一项,系数为1;
(a+b)1=a+b,它有两项,系数分别为1,1;
(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1;
(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1;
…
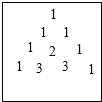
如果将上述每个式子的各项系数排成如图的表格,我们可以发现一些规律,聪明的你一定也发现了,请你根据发现的规律解答下面的问题:
(1)尝试写出(a+b)4的结果,并用整式乘法的相关知识进行验证;
(2)请直接写出(a+b)5共有___项,各项系数的和等于___;
(3)(a+b)n(n为非负整数)共有___项,各项系数的和等于___.
如果将(a+b)n(n为非负整数)的每一项按字母a的次数由大到小排列,就可以得到下面的等式:
(a+b)0=1,它只有一项,系数为1;
(a+b)1=a+b,它有两项,系数分别为1,1;
(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1;
(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1;
…
如果将上述每个式子的各项系数排成如图的表格,我们可以发现一些规律,聪明的你一定也发现了,请你根据发现的规律解答下面的问题:

(1)尝试写出(a+b)4的结果,并用整式乘法的相关知识进行验证;
(2)请直接写出(a+b)5共有___项,各项系数的和等于___;
(3)(a+b)n(n为非负整数)共有___项,各项系数的和等于___.
▼优质解答
答案和解析
(1)(a+b)4=a4+4a3b+6a2b2+4ab3+b4
验证:(a+b)4
=(a+b)2(a+b)2
=(a2+2ab+b2)(a2+2ab+b2)
=a4+4a3b+6a2b2+4ab3+b4
(2)根据规律可得,(a+b)5共有6项,
各项系数分别为:1,5,10,10,5,1,
它们的和等于32;
故答案为:6,32;
(3)根据规律可得,(a+b)n共有(n+1)项,
∵1=20
1+1=21
1+2+1=22
1+3+3+1=23
∴(a+b)n各项系数的和等于2n
故答案为:n+1,2n
验证:(a+b)4
=(a+b)2(a+b)2
=(a2+2ab+b2)(a2+2ab+b2)
=a4+4a3b+6a2b2+4ab3+b4
(2)根据规律可得,(a+b)5共有6项,
各项系数分别为:1,5,10,10,5,1,
它们的和等于32;
故答案为:6,32;
(3)根据规律可得,(a+b)n共有(n+1)项,
∵1=20
1+1=21
1+2+1=22
1+3+3+1=23
∴(a+b)n各项系数的和等于2n
故答案为:n+1,2n
看了 我们已经知道(a+b)2=a...的网友还看了以下:
请问有没有人读过《朗文英语学术高频词汇》(focusonvocabulary)这本书?我有一本英文 2020-05-17 …
假如你叫李华,今年寒假美国某中学学生将来你校访问,你校学生会征募志愿者与美国学生进行交流,并带领他 2020-05-17 …
哲学中国特色社会主义道路之所以正确,之所以能够引领中国发展进步,关键在于我们既坚持中国特色社会主义 2020-06-07 …
用一句话概括下面语段所透露出来的信息。我国中小学生健康状况较过去虽有进步,但仍不容乐观。营养学家、 2020-06-11 …
书面表达(本题有1小题;共计15分)假如你是李华,今年寒假美国某中学学生来你学校访问,学校征募志愿 2020-06-21 …
小学数学题1.小齿轮有28个齿,是大齿轮数的5分之1.大齿轮有多少个齿?2.我国2004年上半年进 2020-07-01 …
谁能帮我翻译一句英文!游学绝不是享受,而是一种感受,是人生的体验;走近国际化进程,参与国际化活动“游 2020-11-04 …
近几年我国派往海外的留学生学成不回国的现象比较突出,这种现象对我国而言()A.可缓解就业压力B.可减 2020-11-14 …
语言运用(12分)中国学生营养与健康促进会于2011年5月14日发布报告称,我国中小学生的早餐质量呈 2020-11-14 …
目前,世界前500强有400多家在我国安家落户,有的准备将总部迁到中国。外资经济的发展对我国经济的积 2020-12-06 …