公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”．利用“割圆术”刘徽得到了圆周率精确到小数点后两位的

Question

公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”．利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”．如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出的值为（　　）
（参考数据：sin15°≈0.2588，sin7.5°≈0.1305）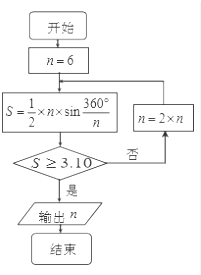

A. 6

B. 12

C. 24

D. 48

Answer 1

模拟执行程序，可得：
n=6，S=3sin60°=(3√(3))/(2)，
不满足条件S≥3.10，n=12，S=6×sin30°=3，
不满足条件S≥3.10，n=24，S=12×sin15°≈12×0.2588=3.1056，
满足条件S≥3.10，退出循环，输出n的值为24．
故选：C．