类比、转化、分类讨论等思想方法和数学基本图形在数学学习和解题中经常用到，如下是一个案例，请补充完整。原题：如图1，在⊙O中，MN是直径，AB⊥MN于点

Question

类比、转化、分类讨论等思想方法和数学基本图形在数学学习和解题中经常用到，如下是一个案例，请补充完整。

原题： 如图 1 ，在⊙ O 中， MN 是直径， AB ⊥ MN 于点 B ， CD ⊥ MN 于点 D ， ∠ AOC =90 °， AB =3 ， CD =4 ，则 BD =            。

⑴尝试探究： 如图 2 ，在⊙ O 中， M N 是直径， AB ⊥ MN 于点 B ， CD ⊥ MN 于点 D ，点 E 在 MN 上，∠ AEC =90 °， AB =3 ， BD =8 ， BE ： DE =1:3 ，则 CD =            （试写出解答过程）。

⑵类比延伸： 利用图 3 ，再探究，当 A 、 C 两点分别在直径 MN 两侧，且 AB ≠ CD ， AB ⊥ MN 于点 B ， CD ⊥ MN 于点 D ，∠ AOC =90 °时，则线段 AB 、 CD 、 BD 满足的数量关系为        。

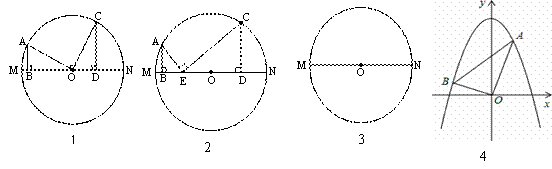⑶拓展迁移： 如图 4 ，在平面直角坐标系中，抛物线经过 A （ m ， 6 ）， B （ n ， 1 ）两点（其中 0 ＜ m ＜ 3 ），且以 y 轴为对称轴，且∠ AOB =90 °，①求 mn 的值；②求抛物线的解析式。

Answer 1

原题： ∵ AB ⊥ MN ， CD ⊥ MN ，

∴∠ ABO= ∠ ODC=90 ° ∠ BAO+ ∠ AOB=90 °

∵∠ AOC=90 °     ∴∠ DOC+ ∠ AOB=90 °

∴∠ BAO= ∠ DOC  又∵ OA=OC ∴△ AOB ≌△ ODC （ AAS ）

∴OD=AB=3，OB=CD=4，∴BD=OB+OD=7

 

尝试探究： ∵ AB ⊥ MN ， CD ⊥ MN ，∴∠ ABE= ∠ CDE=90 °

∠ BAE+ ∠ AEB=90 °∵∠ AEC=90 °∴∠ DEC+ ∠ AEB=90 °

∴∠ BAE= ∠ DEC ∴△ ABE ∽△ EDC

∴

∵ AB=3 ， BD=8 ， BE ： DE=1:3 ，

∴ BE=2，DE=6 ∴ ∴CD=4

⑵类比延伸：

如图 3 （ a ） CD=AB+BD ；

如图 3 （ b ） AB=CD+BD

 

⑶拓展迁移：

①      作 轴于 C 点， 轴于 D 点，

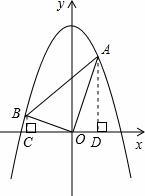
点坐标分别为 ，

∴ ，又∵ ∠ AOB=90 °

∴∠ BCO= ∠ ODA=90 °，∠ OBC= ∠ AOD

∴ ，

∴ 。

②由①得， ，又 ，∴ ，

即 ，

又

∴ 坐标为（ 2 ， 6 ）， B 坐标为（－ 3 ， 1 ），

代入得抛物线解析式为