早教吧作业答案频道 -->物理-->
如图所示的xOy坐标系中,y轴右侧空间存在范围足够大的匀强磁场,磁感应强度大小为B,方向垂直于xOy平面向里.P点的坐标为(-6L,0),Q1、Q2两点的坐标分别为(0,3L),(0,-3L).坐标
题目详情
如图所示的xOy坐标系中,y轴右侧空间存在范围足够大的匀强磁场,磁感应强度大小为B,方向垂直于xOy平面向里.P点的坐标为(-6L,0),Q1、Q2两点的坐标分别为(0,3L),(0,-3L).坐标为(-L,0)处的C点固定一平行于y轴放置一足够长的绝缘弹性挡板,带电粒子与弹性绝缘挡板碰撞前后,沿y方向分速度不变,沿x方向分速度反向,大小不变.带负电的粒子质量为m,电量为q,不计粒子所受重力.若粒子在P点沿PQ1方向进入磁场,经磁场运动后,求:
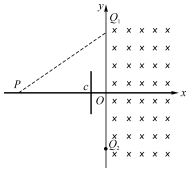
(1)只与挡板碰撞一次并能回到P点的粒子初速度大小;
(2)粒子能否经过坐标原点O之后再回到P点;
(3)只与挡板碰撞三次并能回到P点的粒子初速度大小以及这种情况下挡板的长度至少为多少.

(1)只与挡板碰撞一次并能回到P点的粒子初速度大小;
(2)粒子能否经过坐标原点O之后再回到P点;
(3)只与挡板碰撞三次并能回到P点的粒子初速度大小以及这种情况下挡板的长度至少为多少.
▼优质解答
答案和解析
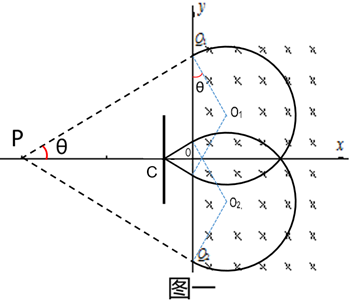 (1)粒子与挡板只碰撞一次,粒子运动的轨迹如图一所示,粒子运动的轨道半径为R,碰撞前后出入磁场两点之间的距离为L
(1)粒子与挡板只碰撞一次,粒子运动的轨迹如图一所示,粒子运动的轨道半径为R,碰撞前后出入磁场两点之间的距离为L
则:根据几何关系可得:4Rcosθ-L=6L,其中:cosθ=
解得:R=
①
根据半径公式:R=
②
联立①②式可得:v=
(2)设粒子在x轴上方与挡板碰撞n次,
每次圆周运动,粒子位置沿y轴向下平移的距离为2Rcosθ,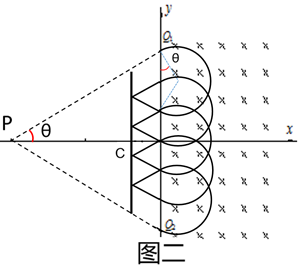
与挡板相碰后,粒子位置向上平移的距离为L,
一次周期性运动粒子沿y轴共向下平移为2Rcosθ-L,
要使粒子经过坐标原点O之后再回到P点需满足:
(n-1)(2Rcosθ-L)+2Rcosθ=3L (n=2,3,4…) ③
联立②③式子可得:v=
(n=2,3,4…)
所以,只要粒子速度满足v=
(n=2,3,4…)粒子就可以经过坐标原点O之后再回到P点(图二为n=2时的过程图)
(3)若与挡板碰撞三次,如图二所示,设挡板的长度L0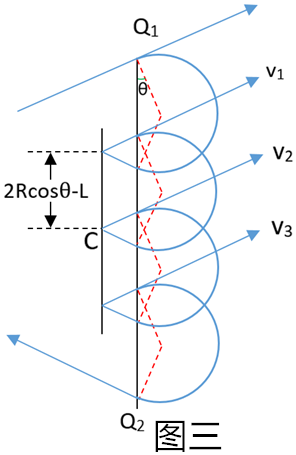
根据几何关系可得:3(2Rcosθ-L)+2Rcosθ=6L
解得:R=
④
根据半径公式:R=
可得:v=
⑤
联立④⑤式子可得:挡板的长度的最小值L0=2(2Rcosθ-L)=2.5L
答:(1)只与挡板碰撞一次并能回到P点的粒子初速度大小为
;
(2)粒子能经过坐标原点O之后再回到P点;
(3)只与挡板碰撞三次并能回到P点的粒子初速度大小以及这种情况下挡板的长度至少为2.5L.
 (1)粒子与挡板只碰撞一次,粒子运动的轨迹如图一所示,粒子运动的轨道半径为R,碰撞前后出入磁场两点之间的距离为L
(1)粒子与挡板只碰撞一次,粒子运动的轨迹如图一所示,粒子运动的轨道半径为R,碰撞前后出入磁场两点之间的距离为L则:根据几何关系可得:4Rcosθ-L=6L,其中:cosθ=
2
| ||
| 5 |
解得:R=
7
| ||
| 8 |
根据半径公式:R=
| mv |
| qB |
联立①②式可得:v=
7
| ||
| 8m |
(2)设粒子在x轴上方与挡板碰撞n次,
每次圆周运动,粒子位置沿y轴向下平移的距离为2Rcosθ,

与挡板相碰后,粒子位置向上平移的距离为L,
一次周期性运动粒子沿y轴共向下平移为2Rcosθ-L,
要使粒子经过坐标原点O之后再回到P点需满足:
(n-1)(2Rcosθ-L)+2Rcosθ=3L (n=2,3,4…) ③
联立②③式子可得:v=
| (n+2)qBL |
| 2nmcosθ |
所以,只要粒子速度满足v=
| (n+2)qBL |
| 2nmcosθ |
(3)若与挡板碰撞三次,如图二所示,设挡板的长度L0

根据几何关系可得:3(2Rcosθ-L)+2Rcosθ=6L
解得:R=
9
| ||
| 16 |
根据半径公式:R=
| mv |
| qB |
9
| ||
| 16m |
联立④⑤式子可得:挡板的长度的最小值L0=2(2Rcosθ-L)=2.5L
答:(1)只与挡板碰撞一次并能回到P点的粒子初速度大小为
7
| ||
| 8m |
(2)粒子能经过坐标原点O之后再回到P点;
(3)只与挡板碰撞三次并能回到P点的粒子初速度大小以及这种情况下挡板的长度至少为2.5L.
看了 如图所示的xOy坐标系中,y...的网友还看了以下:
风险管理的目标分为损失前目标和损失后目标,以下不属于损失前目标的是( )。A.减小事故发生机会B. 2020-05-22 …
从目标实现的时间因素划分,可以将客户理财目标分为( )。A.短期目标B.中期目标C.长期目 2020-05-30 …
宏观调控的目标分为( )。 A.近期目标B.远期目标C.中期目标D.长期目标 2020-05-30 …
美国著名社区工作专家罗夫曼将社区工作的目标分为任务目标和()目标。A.发展B.组织C.社会D.过程 2020-06-04 …
根据指标的性质分类,项目财务评价指标分为时间性指标、比率性指标等,其中价值性指标是指( 2020-06-07 …
条件概率什么时候用19)(本小题满分12分)某人向一目射击4次,每次击中目标的概率为1/3.该目标 2020-06-16 …
在一次射击比赛中,某人向目标射击4次,每次击中目标的概率为,该目标分为红、蓝、黄三个区域,三个区域面 2020-10-30 …
立体几何问题1,在空间指教坐标系o-xyz,点A,B,C坐标分为A(1,0,0),B(0,2,0), 2020-11-07 …
关于教学目标有些教学设计目标分为认识与技能、数学思考、解决问题、情感态度.有些分为知识与技能、过程与 2020-11-14 …
(初中数学分学段目标及内容主线的分析)初中数学分学段目标分为几个方面? 2020-11-22 …