早教吧作业答案频道 -->数学-->
如图,点E是正方形ABCD对角线AC上一点,EC=BC,过点E作FE⊥BE,交CD于点F(Ⅰ)∠BEC的度数等于.(Ⅱ)若正方形的边长为a,则CF的长等于.
题目详情
如图,点E是正方形ABCD对角线AC上一点,EC=BC,过点E作FE⊥BE,交CD于点F
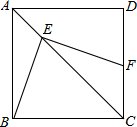
(Ⅰ)∠BEC的度数等于___.
(Ⅱ)若正方形的边长为a,则CF的长等于___.

(Ⅰ)∠BEC的度数等于___.
(Ⅱ)若正方形的边长为a,则CF的长等于___.
▼优质解答
答案和解析
(1)点E是正方形ABCD对角线AC上一点,
∴∠ACB=45°,
∵EC=BC,
∴∠BEC=∠EBC=
=67.5°
故答案为67.5°;
由(1)知,∠CBE=∠BEC=67.5°,
∴∠ABE=22.5°,
∵FE⊥BE,
∴∠BEF=90°,
∴∠CEF=22.5°,
∴∠ABE=∠CEF,
∵∠BAE=∠ECF,
∴△ABE和△CEF中
,
∴△ABE≌△CEF,
∴CF=AE,
∵正方形ABCD的边长为a,
∴AC=
a,
∵CE=AB=a,
∴CF=AE=AC-CE=
a-a=(
-1)a,
故答案为(
-1)a.
∴∠ACB=45°,
∵EC=BC,
∴∠BEC=∠EBC=
| 180°-∠ACB |
| 2 |
故答案为67.5°;
由(1)知,∠CBE=∠BEC=67.5°,
∴∠ABE=22.5°,
∵FE⊥BE,
∴∠BEF=90°,
∴∠CEF=22.5°,
∴∠ABE=∠CEF,
∵∠BAE=∠ECF,
∴△ABE和△CEF中
|
∴△ABE≌△CEF,
∴CF=AE,
∵正方形ABCD的边长为a,
∴AC=
| 2 |
∵CE=AB=a,
∴CF=AE=AC-CE=
| 2 |
| 2 |
故答案为(
| 2 |
看了如图,点E是正方形ABCD对角...的网友还看了以下:
已知,如图∠A=∠C,CD丄AB于D,交AE于F,试断定ΔAEB的形状,并说明你的结论的合理性.AD 2020-03-30 …
设栈的初始为空,元素a,b,c,d,e,f,g依次入栈,以下出栈序列不可能出现的是A,a,b,c, 2020-05-17 …
设栈S的初始状态为空,元素a,b,c,d,e,f依次入栈S,出栈的序列为b,d,f,e,c,a…… 2020-05-17 …
设有关系模式R(A,B,C,D,E,F) ,其函数依赖集为F={E→D,C→B,CE→F,B→A}。 2020-05-23 …
设有关系模式R(A,B,C,D,E,F) ,其函数依赖集为F={E→D,C→B,CE→F,B→A}。 2020-05-23 …
设有关系模式R(A,B,C,D,E,F),其函数依赖集为F={E→D,C→B,CE→F,B→A}。则 2020-05-24 …
设有关系模式R(A,B,C,D,E,F),根据语义有如下函数依赖集:F={A→B,(C,D) →A, 2020-05-24 …
关系模式R(U,F),其中U={A,B,C,D,E},F={AC→E,E→D,A→B,B→D}。关系 2020-05-26 …
如图,矩形ABCD中,AD=3cm,AB=2cm,点E沿A→D方向移动,点F沿D→A方向移动,速度 2020-06-06 …
EXCEL循环或计算问题。F=A+B+C+D+E。(A.B.C.D.E.F.均要大于零)E=A*10 2020-11-01 …