早教吧作业答案频道 -->数学-->
将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG,(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;(2)若AB=8,AD=4,求四边形DHBG的
题目详情
将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG,
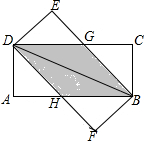
(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB=8,AD=4,求四边形DHBG的面积.

(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB=8,AD=4,求四边形DHBG的面积.
▼优质解答
答案和解析
(1)四边形DHBG是菱形.理由如下:
∵四边形ABCD、FBED是完全相同的矩形,
∴∠A=∠E=90°,AD=ED,AB=EB.
在△DAB和△DEB中,
,
∴△DAB≌△DEB(SAS),
∴∠ABD=∠EBD.
∵AB∥CD,DF∥BE,
∴四边形DHBG是平行四边形,∠HDB=∠EBD,
∴∠HDB=∠HBD,
∴DH=BH,
∴▱DHBG是菱形.
(2)由(1),设DH=BH=x,则AH=8-x,
在Rt△ADH中,AD2+AH2=DH2,即42+(8-x)2=x2,
解得:x=5,即BH=5,
∴菱形DHBG的面积为HB•AD=5×4=20.
∵四边形ABCD、FBED是完全相同的矩形,
∴∠A=∠E=90°,AD=ED,AB=EB.
在△DAB和△DEB中,
|
∴△DAB≌△DEB(SAS),
∴∠ABD=∠EBD.
∵AB∥CD,DF∥BE,

∴四边形DHBG是平行四边形,∠HDB=∠EBD,
∴∠HDB=∠HBD,
∴DH=BH,
∴▱DHBG是菱形.
(2)由(1),设DH=BH=x,则AH=8-x,
在Rt△ADH中,AD2+AH2=DH2,即42+(8-x)2=x2,
解得:x=5,即BH=5,
∴菱形DHBG的面积为HB•AD=5×4=20.
看了将两张完全相同的矩形纸片ABC...的网友还看了以下:
(2010•本溪)我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形. 2020-05-12 …
给出定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.(1) 2020-05-13 …
我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形,请解答下列问题:( 2020-05-14 …
我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.写出你所学过的特殊 2020-05-14 …
已知如图在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥BD交CB的延 2020-05-15 …
已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB 2020-05-15 …
已知角abcd是平行四边形,ef是对角线上的两,且be=df,连接ae.af.ce.cf;判断四边 2020-05-16 …
特殊的方法求特殊四边形面积的方法比如说对角线相互垂直的四边形面积等于二分之一对角线乘积不要那种平行 2020-06-02 …
分一分.(1)画一条线段将平行四边形分成两个三角形.(2)画一条线段将平行四边形分成两个平行四边形 2020-08-02 …
求四边形AODE是什么特殊四边形?为什么?在矩形ABCD中,AC,BD相交于点O,如果分别过点A,D 2021-01-22 …