早教吧作业答案频道 -->数学-->
抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形,阿基米德三角形有一些有趣的性质,如:若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线
题目详情
抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形,阿基米德三角形有一些有趣的性质,如:若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上.设抛物线y 2 =2px(p>0),弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为( )
A.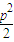
B.p 2
C.2p 2
D.4p 2
A.
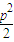
B.p 2
C.2p 2
D.4p 2
▼优质解答
答案和解析
分析:
法一:直接计算比较复杂,我们可以取几个特殊的位置,可得解.
法二:由于若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上,且△PAB为直角三角型,且角P为直角.又面积是直角边积的一半,斜边是两直角边的平方和,故可求.
法一:取倾斜角为:45 ,60 ,90 ,经计算可知,当倾斜角为90 时,△ABQ的面积的最小,此时AB=2p,又焦点到准线的距离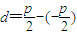 =p,此时三角形的面积最小为p 2 故选B.
=p,此时三角形的面积最小为p 2 故选B.
法二:由于若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上,且△PAB为直角三角型,且角P为直角.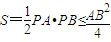 ,由于AB是通径时,AB最小,故选B.
,由于AB是通径时,AB最小,故选B.
点评:
本题作为选择题,采用特殊法,简单易行.由特殊求解一般性结论是解答选择题的一种很好的方法.△PAB称作阿基米德三角型.该三角形满足以下特性:1、P点必在抛物线的准线上;2、△PAB为直角三角型,且角P为直角;3、PF⊥AB(即符合射影定理)等.灵活利用性质是解题的关键.
分析:
法一:直接计算比较复杂,我们可以取几个特殊的位置,可得解.
法二:由于若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上,且△PAB为直角三角型,且角P为直角.又面积是直角边积的一半,斜边是两直角边的平方和,故可求.
法一:取倾斜角为:45 ,60 ,90 ,经计算可知,当倾斜角为90 时,△ABQ的面积的最小,此时AB=2p,又焦点到准线的距离
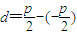 =p,此时三角形的面积最小为p 2 故选B.
=p,此时三角形的面积最小为p 2 故选B.法二:由于若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上,且△PAB为直角三角型,且角P为直角.
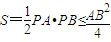 ,由于AB是通径时,AB最小,故选B.
,由于AB是通径时,AB最小,故选B.点评:
本题作为选择题,采用特殊法,简单易行.由特殊求解一般性结论是解答选择题的一种很好的方法.△PAB称作阿基米德三角型.该三角形满足以下特性:1、P点必在抛物线的准线上;2、△PAB为直角三角型,且角P为直角;3、PF⊥AB(即符合射影定理)等.灵活利用性质是解题的关键.
看了 抛物线的弦与过弦的端点的两条...的网友还看了以下:
某哺乳动物的基因型为MMNn,该动物减数分裂形成的一个基因型为MmN的配子如图所示,下列关于该配子 2020-04-07 …
对基因文库的描述,正确的是()A.cDNA文库的基因中有内含子和启动子B.可根据基因的功能从基因文 2020-04-08 …
转基因有害的理论依据是什么据我了解每种动物和植物的基因都是不同的,并且丰富多样的物种就是在进化过程 2020-04-27 …
麻雀与汽车的根本区别在于麻雀是生物,具有生物的基本特征.下列不属于生物基本特征的是()A.生物都能 2020-05-13 …
生物的基本特征有哪些?请全部回答出下列不属于生物基本特征的是?A、生物的生活需要营养 B、生物都能 2020-05-16 …
转基因技术的定义()转基因生物就是将某些生物的基因转移到其他物种中去,改造生物的遗传物质,使其在性 2020-05-17 …
某种植物的基因型为AABb,去雄蕊后授以基因型为aabb植物的花粉,其胚乳可能的基因型是()A.A 2020-05-17 …
基因种类某种二倍体植物的1号染色体上控制花色的等位基因共有4种,2号染色体上控制茎高矮的等位基因共 2020-05-17 …
真核生物的基因转到真核生物中要把内含子去掉吗?真核生物的基因转到原核生物中要把内含子去掉.真核生物 2020-05-17 …
怎样形容宇宙?宇宙无边阿,物质基础… 2020-06-11 …