早教吧作业答案频道 -->物理-->
如图所示,轨道a、b、c在同一竖直平面内,其中a是光滑圆弧轨道且末端水平,b是半径为r=2m的光滑半圆形轨道且直径DF沿竖直方向,水平轨道c上静止放置着相距l=1.0m的物块B和C,B位于F处,现
题目详情
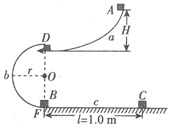
如图所示,轨道a、b、c在同一竖直平面内,其中a是光滑圆弧轨道且末端水平,b是半径为r=2m的光滑半圆形轨道且直径DF沿竖直方向,水平轨道c上静止放置着相距l=1.0m的物块B和C,B位于F处,现将小球A从轨道a距D点高为H的位置由静止释放,小球经D处水平进入轨道b后恰能沿轨道内侧运动,到达F处与物块B正碰,碰后A、B粘在一起向右滑动,并与C发生弹性正碰.已知A、B、C质量分别为m,m,6m均可看做质点,物块与地面的动摩擦因数μ=0.45.(设碰撞时间很短,g取10m/s2)
(1)求H的大小;
(2)求物块C与AB整体都停止运动后它们之间的距离.

(1)求H的大小;
(2)求物块C与AB整体都停止运动后它们之间的距离.
▼优质解答
答案和解析
(1)滑块A从轨道a下滑到达D点的过程中,由机械能守恒定律得:
mgH=
mvD2,
要使滑块A恰好能沿竖直平面内光滑半圆轨道b内侧做圆周运动,在D点应满足:
mg=
,
联立并代入数据解得 H=1m.
(2)滑块A从a轨道上H=1m处下滑到达F点的过程,由机械能守恒定律得
mg(H+2r)=
m
可得,滑块经过F点的速度 v0=10m/s
A、B碰撞过程,取向右为正方向,由动量守恒定律得:
mv0=2mv1.
设AB整体与C碰撞前瞬间的速度为v2.由动能定理得:
-μ•2mgl=
•2m
-
•2m
联立以上各式解得 v2=4m/s
AB整体与C发生弹性碰撞,由动量守恒定律和能量守恒定律得:
2mv2=2mv3+6mv
×2mv22=
×2mv32+
•6mv42
解得 v3=-2m/s,v4=2m/s
此时AB整体的运动方向与C相反,速度的大小相等.
A与B的整体向左做减速运动,位移的大小:xAB=
代入数据得:xAB=
m
C向右做减速运动的位移:xc=
代入数据得:xc=
m
所以AB与C之间的距离:L=xAB+xC=
m+
m=
m
答:(1)H的大小是1m;
(2)物块C与AB整体都停止运动后它们之间的距离是
m.
mgH=
| 1 |
| 2 |
要使滑块A恰好能沿竖直平面内光滑半圆轨道b内侧做圆周运动,在D点应满足:
mg=
m
| ||
| r |
联立并代入数据解得 H=1m.
(2)滑块A从a轨道上H=1m处下滑到达F点的过程,由机械能守恒定律得
mg(H+2r)=
| 1 |
| 2 |
| v | 2 0 |
可得,滑块经过F点的速度 v0=10m/s
A、B碰撞过程,取向右为正方向,由动量守恒定律得:
mv0=2mv1.
设AB整体与C碰撞前瞬间的速度为v2.由动能定理得:
-μ•2mgl=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
联立以上各式解得 v2=4m/s
AB整体与C发生弹性碰撞,由动量守恒定律和能量守恒定律得:
2mv2=2mv3+6mv
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得 v3=-2m/s,v4=2m/s
此时AB整体的运动方向与C相反,速度的大小相等.
A与B的整体向左做减速运动,位移的大小:xAB=
| ||||
| 2μmg |
代入数据得:xAB=
| 4 |
| 9 |
C向右做减速运动的位移:xc=
| ||||
| 6μmg |
代入数据得:xc=
| 4 |
| 9 |
所以AB与C之间的距离:L=xAB+xC=
| 4 |
| 9 |
| 4 |
| 9 |
| 8 |
| 9 |
答:(1)H的大小是1m;
(2)物块C与AB整体都停止运动后它们之间的距离是
| 8 |
| 9 |
看了 如图所示,轨道a、b、c在同...的网友还看了以下:
关于一个对数函数的增减性的问题f(x)=log(a-a^x)(a>1)其中为对数函数的底数a^x为 2020-04-25 …
见图(1)中为什么不可以这样写第一次达到最大值的时候t=T/3那么t=T/3时候v可以达到最大值那 2020-04-26 …
不饱和度的计算方法的问题1.根据有机物分子结构计算,Ω=双键数+叁键数×2+环数2.立体封闭有机物 2020-05-16 …
在f(x)=1/x与f(x)=1/(x)²中为什么存在或不存在极限?如何在不画图情况下判断以上的情 2020-05-16 …
在f(x)=1/x与f(x)=1/(x)²中为什么存在或不存在极限?如何在不画图情况下判断以上的情 2020-05-16 …
状语从句翻译2个10分1.Shedidtheworkashewastold2.Hespokeasi 2020-05-17 …
西语的一些问题1,conocemosaestosjovenes中为什么要加“a”,conocemo 2020-05-20 …
把-5,-4,-3,-2,-1,0,1,2,3填入九宫格内,使每行、每列、对角之和相等我自己琢磨出 2020-06-10 …
同济6高数极限准则中例题四分之一圆1-32中,为什么X=弧AB,为什么扇形AOB面积=二分之一的X 2020-06-10 …
下图表示病菌感染人体后,免疫细胞做出应答的部分过程,请据图回答问题。(1)图中②为细胞,④为细胞。 2020-06-19 …