已知函数f（x）=x2-4|x|+3．（1）试证明函数f（x）是偶函数；（2）画出f（x）的图象；（要求先用铅笔画出草图，再用中性笔描摹）（3）请根据图象指出函数f（x）的单调递增区间与单调递减

Question

已知函数f（x）=x²-4|x|+3．
（1）试证明函数f（x）是偶函数；
（2）画出f（x）的图象；（要求先用铅笔画出草图，再用中性笔描摹）
（3）请根据图象指出函数f（x）的单调递增区间与单调递减区间；（不必证明）
（4）当实数k取不同的值时，讨论关于x的方程x²-4|x|+3=k的实根的个数．

Answer 1

（1）由于函数f（x）=x²-4|x|+3的定义域为R，
关于原点对称，
且满足f（-x）=（-x）²-4|-x|+3=x²-4|x|+3=f（x），
故函数 f（x）是偶函数．
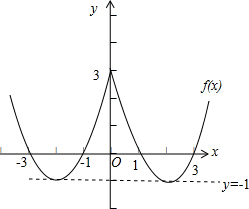
（2）f（x）的图象如图所示：
（3）根据图象指出函数f（x）的单调递增区间
为[-2，0]、[2，+∞）；
单调递减区间为（-∞，-2]、[0，2]．
（4）当实数k取不同的值时，
讨论关于x的方程x²-4|x|+3=k的实根的个数，
即函数y=x²-4|x|+3的图象和直线y=k交点的个数．
由图象可看出，当k<-1时，方程实根的个数为0；
当k=-1时，方程实根的个数为2；
当-1当k=3时，方程实根个数为3；
当k>3时，方程实根个数为2．