如图，静止于A处的离子，经电压为U的加速电场加速后沿图中圆弧虚线通过静电分析器，从P点垂直CN进入矩形区域的有界匀强电场，电场方向水平向左．静电分析器通道内有均匀辐向分布的

Question

如图，静止于A处的离子，经电压为U的加速电场加速后沿图中圆弧虚线通过静电分析器，从P点垂直CN进入矩形区域的有界匀强电场，电场方向水平向左．静电分析器通道内有均匀辐向分布的电场，已知圆弧所在处场强为E₀，方向如图所示；离子质量为m、电荷量为q；

.

QN

=2d、

.

PN

=3d，离子重力不计．

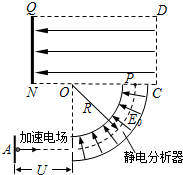
（1）求圆弧虚线对应的半径R的大小；
（2）若离子恰好能打在NQ的中点上，求矩形区域QNCD内匀强电场场强E的值；
（3）若撤去矩形区域QNCD内的匀强电场，换为垂直纸面向里的匀强磁场，要求离子能最终打在QN上，求磁场磁感应强度B的取值范围．

Answer 1

（1）离子在加速电场中加速，根据动能定理，有：qU=(1)/(2)mv2，
离子在辐向电场中做匀速圆周运动，电场力提供向心力，根据牛顿第二定律有：qE0=m(v2)/(R)，
解得：R=(2U)/(E0)；
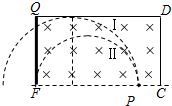
（2）离子做类平抛运动：
d=vt
3d=(1)/(2)at2
由牛顿第二定律得：qE=ma，
解得：E=(12U)/(d)；
（3）离子在匀强磁场中做匀速圆周运动，洛伦兹力提供向心力，根据牛顿第二定律有：qBv=m(v2)/(r)，
解得：r=(1)/(B)√((2Um)/(q))，
离子能打在QN上，则既没有从DQ边出去也没有从PN边出去，则离子运动径迹的边界如图中Ⅰ和Ⅱ．
由几何关系知，离子能打在QN上，必须满足：(3)/(2)d<r≤2d，
则有：(1)/(2d)√((2Um)/(q))≤B<(2)/(3d)√((2Um)/(q))；
答：（1）圆弧虚线对应的半径R的大小为(2U)/(E0)；
（2）若离子恰好能打在NQ的中点上，矩形区域QNCD内匀强电场场强E的值为(12U)/(d)；
（3）磁场磁感应强度B的取值范围是(1)/(2d)√((2Um)/(q))≤B<(2)/(3d)√(作业帮用户2018-02-01举报扫描下载二维码©2019 作业帮 联系方式：[e-mail]作业帮协议)