早教吧作业答案频道 -->数学-->
如图,点A,C,E在一条直线上,已知ABC和△EDC都是等边三角形,AD,BE相交于点O,AD,BC相交于点F,CD,BE相交于点G.连接FG和OC.(1)试证明:AD=BE;(2)小明认为还可以得到如下结论:①A
题目详情
如图,点A,C,E在一条直线上,已知ABC和△EDC都是等边三角形,AD,BE相交于点O,AD,BC相交于点F,CD,BE相交于点G.连接FG和OC.
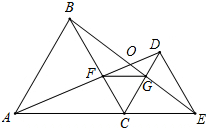
(1)试证明:AD=BE;
(2)小明认为还可以得到如下结论:①AF=BG;②FG∥AE;③∠AOC=∠EOC.你认为其中正确的有___(填序号即可).并选择一个正确结论进行证明;
(3)试猜想线段OC,OD,OE之间有何数量关系?并证明你的猜想的正确性.

(1)试证明:AD=BE;
(2)小明认为还可以得到如下结论:①AF=BG;②FG∥AE;③∠AOC=∠EOC.你认为其中正确的有___(填序号即可).并选择一个正确结论进行证明;
(3)试猜想线段OC,OD,OE之间有何数量关系?并证明你的猜想的正确性.
▼优质解答
答案和解析
证明:(1)∵△ABC和△CDE都是等边三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,
即∠BCE=∠ACD,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴AD=BE;
(2)正确的有①②③,
证明:连接OC,
 ∵∠AOB+∠ABO+∠BAO=180°,∠OBC=∠CAO,
∵∠AOB+∠ABO+∠BAO=180°,∠OBC=∠CAO,
∴∠AOB+∠ABC+∠BAC=180°,
∴∠AOB=60°,
∵∠EOD+∠EDO+∠OED=180°,
∴∠ODC+∠DEO=60°,
∴∠ODC=∠CEO,
同理∠OCD=∠DEO,
∴∠COE=60°,
同理∠AOC=60°,
∴∠AOC=∠EOC;故③正确;
∵∠FGD+∠DFG+∠FDG=180°,
∵∠DFG=∠DEO,∠FDG=∠CEO,
∴∠DFG+∠FDG=60°
∴∠FGD=∠ACD=120°,
∴PQ∥AE,故②正确;
∵FG∥AE
∴∠CFG=∠ACB=60°,
∵∠FCG=60°,
∴△CFG为等边三角形,
∴CF=CG,
在△ACF与△BCG中,
,
∴△ACF≌△BCG,
∴AF=BG;故①正确;
故答案为:①②③;
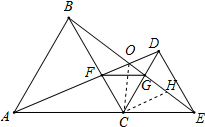
(3)在OE上截取OH=OC,
∵∠COE=60°,
∴OC=OH=CH,
∴∠OCH=60°,
∴∠OCG=∠HCE,
在△OCD与△HCE中,
,
∴△OCD≌△HCE,
∴HE=OD,
∵OE=OH+HE,
∴OE=OC+OD.
∴AC=BC,CE=CD,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,
即∠BCE=∠ACD,
在△BCE和△ACD中,
|
∴△BCE≌△ACD(SAS),
∴AD=BE;
(2)正确的有①②③,
证明:连接OC,
 ∵∠AOB+∠ABO+∠BAO=180°,∠OBC=∠CAO,
∵∠AOB+∠ABO+∠BAO=180°,∠OBC=∠CAO,∴∠AOB+∠ABC+∠BAC=180°,
∴∠AOB=60°,
∵∠EOD+∠EDO+∠OED=180°,
∴∠ODC+∠DEO=60°,
∴∠ODC=∠CEO,
同理∠OCD=∠DEO,
∴∠COE=60°,
同理∠AOC=60°,
∴∠AOC=∠EOC;故③正确;
∵∠FGD+∠DFG+∠FDG=180°,
∵∠DFG=∠DEO,∠FDG=∠CEO,
∴∠DFG+∠FDG=60°
∴∠FGD=∠ACD=120°,
∴PQ∥AE,故②正确;
∵FG∥AE
∴∠CFG=∠ACB=60°,
∵∠FCG=60°,
∴△CFG为等边三角形,
∴CF=CG,
在△ACF与△BCG中,
|
∴△ACF≌△BCG,
∴AF=BG;故①正确;
故答案为:①②③;
(3)在OE上截取OH=OC,
∵∠COE=60°,
∴OC=OH=CH,
∴∠OCH=60°,
∴∠OCG=∠HCE,
在△OCD与△HCE中,
|
∴△OCD≌△HCE,
∴HE=OD,
∵OE=OH+HE,
∴OE=OC+OD.
看了如图,点A,C,E在一条直线上...的网友还看了以下:
相似三角形:如图,已知在平行四边形ABCD中,E为AB边的中点,AF=1/2FD,FE与AC相交于 2020-05-16 …
小周通过实验探究物体的重力与质量的关系.记录的数据如下表,请你以质量m为横坐标,以重力G为纵坐标, 2020-06-21 …
有下列结论:①相等的角在直观图中仍然相等;②相等的线段在直观图中仍然相等;③若两条线段平行,则在直 2020-06-27 …
根据如图回答下列问题:(1)图中结构G、H和J构成一个肾单位.(2)在尿的形成过程中要经过两个作用 2020-07-01 …
如图1,若AB∥CD,则有∠B+∠D=∠E.1.将点E移至图2的位置时,∠D,∠B,∠E有什么关系 2020-07-20 …
为保护环境,国家实施退耕还林工程,图中F,G两处相比,优先退耕还林的是G原因:F,G相比,G处等高线 2020-11-10 …
(2014•邢台二模)已知函数f(x)=b(x+1)lnx-x+1,斜率为l的直线与函数f(x)的图 2020-11-12 …
已知两个分段函数f(x)和g(x),求f(g(x))只要讨论g(x)的取值范围而求f(f(x))却需 2020-12-23 …
如表内容与结论不相对应的是()内容结论A一个反应的△H>0,△S>0反应一定不能自发进行B硝酸铵溶于 2020-12-23 …
关于自由落体加速度g,下列说法正确的是()A.同一物体不论什么地点g相等B.重的物体与轻的物体相比较 2021-01-22 …