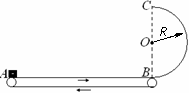
如图所示,水平传送带上A、B两端点间距L=4m,半径R=1m的光滑半圆形轨道固定于竖直平面内,下端与传送带B相切。传送带以v0=4m/s的速度沿图示方向匀速运动,质量m=1kg的小滑
如图所示,水平传送带上 A 、 B 两端点间距 L = 4m,半径 R =1m的光滑半圆形轨道固定于竖直平面内,下端与传送带 B 相切。传送带以 v 0 = 4m/s的速度沿图示方向匀速运动,质量 m =1kg的小滑块由静止放到传送带的 A 端,经一段时间运动到 B 端,滑块与传送带间的动摩擦因数 μ = 0.5,取 g =10m/s 2 。
⑴求滑块到达 B 端的速度;
⑵求滑块由 A 运动到 B 的过程中,滑块与传送带间摩擦产生的热量;
⑶仅改变传送带的速度,其他条件不变,计算说明滑块能否通过圆轨道最高点 C 。
⑴滑块在传送带上先向右做加速运动,设当速度 v = v 0 时已运动的距离为 x
根据动能定理  (2分)
(2分)
得 x =1.6m< L , 所以滑块到达 B 端时的速度为4m/s (2分)
⑵设滑块与传送带发生相对运动的时间为 t ,则  (1分)
(1分)
滑块与传送带之间产生的热量  (2分)
(2分)
解得 Q = 8J (2分)
⑶设滑块通过最高点 C 的最小速度为 
经过 C 点:根据向心力公式 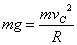 (2分)
(2分)
从 B 到 C 过程:根据动能定理  (2分)
(2分)
解得 经过 B 的速度  m/s
m/s
从 A 到 B 过程:若滑块一直加速,根据动能定理 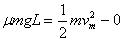 (2分)
(2分)
解得 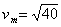 m/s
m/s
由于速度 v m < v B ,所以仅改变传送带的速度,滑块不能通过圆轨道最高点 (1分)
注:其他正确解法同样给分
一个点为((4k+4)/k^2,4/k),怎样写出其方程即y关于x的表达式x=y+(y^2一个点为 2020-04-25 …
一,已知A={x|x=k/4+1/2,k∈Z} B={x|x=k/8+1/4,k∈Z}那么集合A与 2020-05-16 …
因为81=3^4,所以3^k+1=3^4则k+1=4,k=3.因为3^k+1=3^k乘3=81,所 2020-05-17 …
甲乙两人玩纸牌游戏从足够数量的纸牌中取牌规定每人最多两种取法,甲每次取4张或(4-k)张,乙每次取 2020-06-06 …
已知a,b是方程x^2-2(k-1)x+k+1=0的两实根……已知a,b是方程x^2-2(k-1) 2020-06-07 …
已知集合A={x|x=k+1/4,k∈Z},B={x|x=k/2-1/4,k∈Z},C={x|x= 2020-06-26 …
K系与K’系是坐标轴相互平行的两个惯性系,K’系相对于K系沿OX轴正方向匀速运动.一根刚性尺静止在 2020-07-31 …
4+k^2)x^2-2k(2+k)x+(k+2)^2-8=0x=k(2+k)/(k^2+4)(k^ 2020-08-02 …
1+2+3+4+5+.+n=0.5n^2+n1^2+2^2+3^2.+n^2=n(n+1)(2n+ 2020-08-03 …
设集合M={x|x=(kπ/2)+(π/4),k∈Z},N={x|x=(kπ/4)+(π设集合M={ 2021-01-13 …