早教吧作业答案频道 -->数学-->
一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面
题目详情
一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
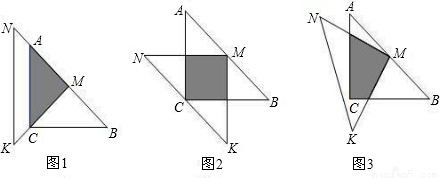
(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为______,周长为______

(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为______,周长为______
▼优质解答
答案和解析
分析:
(1)由等腰直角三角形的性质:底边上的中线与底边上的高重合,得到△AMC是等腰直角三角形,AM=MC=AC=a,则重叠部分的面积是△ACB的面积的一半,为a2,周长为(1+)a.(2)易得重叠部分是正方形,边长为a,面积为a2,周长为2a.(3)过点M分别作AC、BC的垂线MH、MG,垂足为H、G.求得Rt△MHE≌Rt△MGF,则阴影部分的面积等于正方形CGMH的面积.
(1)∵AM=MC=AC=a,则∴重叠部分的面积是△ACB的面积的一半为a2,周长为(1+)a.(2)∵叠部分是正方形∴边长为a,面积为a2,周长为2a.(3)猜想:重叠部分的面积为.理由如下:过点M分别作AC、BC的垂线MH、MG,垂足为H、G设MN与AC的交点为E,MK与BC的交点为F∵M是△ABC斜边AB的中点,AC=BC=a∴MH=MG=又∵∠HME+∠HMF=∠GMF+∠HMF,∴∠HME=∠GMF,∴Rt△MHE≌Rt△MGF∴阴影部分的面积等于正方形CGMH的面积∵正方形CGMH的面积是MG?MH=×=∴阴影部分的面积是.
点评:
本题利用了等腰直角三角形的性质,等腰直角三角形的面积公式,正方形的面积公式,全等三角形的判定和性质求解.
分析:
(1)由等腰直角三角形的性质:底边上的中线与底边上的高重合,得到△AMC是等腰直角三角形,AM=MC=AC=a,则重叠部分的面积是△ACB的面积的一半,为a2,周长为(1+)a.(2)易得重叠部分是正方形,边长为a,面积为a2,周长为2a.(3)过点M分别作AC、BC的垂线MH、MG,垂足为H、G.求得Rt△MHE≌Rt△MGF,则阴影部分的面积等于正方形CGMH的面积.
(1)∵AM=MC=AC=a,则∴重叠部分的面积是△ACB的面积的一半为a2,周长为(1+)a.(2)∵叠部分是正方形∴边长为a,面积为a2,周长为2a.(3)猜想:重叠部分的面积为.理由如下:过点M分别作AC、BC的垂线MH、MG,垂足为H、G设MN与AC的交点为E,MK与BC的交点为F∵M是△ABC斜边AB的中点,AC=BC=a∴MH=MG=又∵∠HME+∠HMF=∠GMF+∠HMF,∴∠HME=∠GMF,∴Rt△MHE≌Rt△MGF∴阴影部分的面积等于正方形CGMH的面积∵正方形CGMH的面积是MG?MH=×=∴阴影部分的面积是.
点评:
本题利用了等腰直角三角形的性质,等腰直角三角形的面积公式,正方形的面积公式,全等三角形的判定和性质求解.
看了一位同学拿了两块45°的三角尺...的网友还看了以下:
在粗糙水平面上放一个三角形木块A,若物体B在A的斜面上匀速下滑,则A.木块A保持静止,有相对水平面 2020-04-26 …
现有a×a、b×b的正方形纸片(a≠b)和a×b的矩形纸片若干块.现选用一块a×a、三块b×b的正 2020-05-17 …
如图所示,物块A放在木板上处于静止状态,现将木块B略向右移动一些,使倾角α减小,则下列结论正确的是 2020-05-17 …
)如图所示,木块B与竖直墙C相接触,木块A放置在木块B上,在竖直向上的力F的作用下,木如图所示,木 2020-05-17 …
在进行学生比赛管理信息系统设计师有两个模块A和B,模块A调用模块B时需要传递整形参数,这种耦合方式是 2020-05-24 …
如图所示,A、B、C三木块质量相等,一切接触面光滑,一子弹由A射入,从B射出,则三木块速度情况() 2020-06-05 …
A想买一包烟,可她没钱,于是和B借了50和C借了50,现在她就有100块了,买了一包97块的烟,剩 2020-07-10 …
如图所示,物块A放在木板上处于静止状态,现将木块B略向右移动一些,使倾角α减小,则下列结论正确的是 2020-07-13 …
如图所示,A、B两木块靠在一起放于光滑的水平面上,A、B的质量均为m=2kg.一个质量mc=1kg 2020-07-20 …
如图16-6-4所示,木块A和B叠放在水平面上,轻推木块B,A会与B一起运动,猛击木块B,B将从A下 2020-12-03 …