如图，某构件是由编号1、2、…、k（k∈N*且k≥3）的有限个圆柱自下而上组成的，其中每一个圆柱的高与其底面圆的直径相等，且对于任意两个相邻圆柱，上面圆柱的高是下面圆柱的高的一

Question

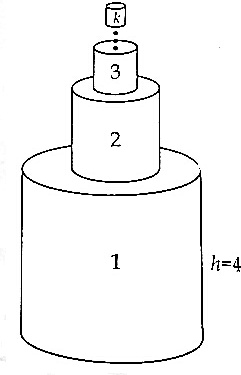
如图，某构件是由编号1、2、…、k（k∈N^*且k≥3）的有限个圆柱自下而上组成的，其中每一个圆柱的高与其底面圆的直径相等，且对于任意两个相邻圆柱，上面圆柱的高是下面圆柱的高的一半，设编号1的圆柱的高为4．

（1）分别求编号1、编号2的圆柱的体积V₁、V₂；
（2）写出编号n（n=1，2，…，k）的圆柱的体积V_n关于n的表达式（不必证明）；
（3）求该构件的体积．

Answer 1

（1）V₁=π×2²×4=16π，V₂=π×1²×2=2π，
（2）设编号为n的圆柱的高为h_n，则数列{h_n}为以4为首项，(1)/(2)为公比的等比数列，
∴h_n=4×((1)/(2))n-1=(1)/(2n-3)．∴编号为n的圆柱的底面半径为(1)/(2n-2)．
∴V_n=π×((1)/(2n-2))2×(1)/(2n-3)=(1)/(23n-7)π．
（3）∵(Vn+1)/(Vn)=(π)/(23(n+1)-7)×(23n-7)/(π)=(1)/(8)，
∴数列{V_n}是以16π为首项，以(1)/(8)为公比的等差数列，
∴几何体的体积为S_k=(16π(1-(1)/(8k)))/(1-(1)/(8))=(128π)/(7)（1-(1)/(8k)）．