早教吧作业答案频道 -->数学-->
已知二次函数y=x2-2ax-2a-6(a为常数,a≠0).(1)求证:该二次函数的图象与x轴有两个交点;(2)设该二次函数的图象与x轴交于点A(-2,0)和点B,与y轴交于点C,线段BC的垂直平分线l与x轴
题目详情
已知二次函数y=x2-2ax-2a-6(a为常数,a≠0).
(1)求证:该二次函数的图象与x轴有两个交点;
(2)设该二次函数的图象与x轴交于点A(-2,0)和点B,与y轴交于点C,线段BC的垂直平分线l与x轴交于点D.
①求点D的坐标;
②设点P是抛物线上的一个动点,点Q是直线l上的一个动点.以点B、D、P、Q为顶点的四边形是否可能为平行四边形?若能,直接写出点Q的坐标.
(1)求证:该二次函数的图象与x轴有两个交点;
(2)设该二次函数的图象与x轴交于点A(-2,0)和点B,与y轴交于点C,线段BC的垂直平分线l与x轴交于点D.
①求点D的坐标;
②设点P是抛物线上的一个动点,点Q是直线l上的一个动点.以点B、D、P、Q为顶点的四边形是否可能为平行四边形?若能,直接写出点Q的坐标.
▼优质解答
答案和解析
(1)证明:y=x2-2ax-2a-6
当a≠0时,(-2a)2-4(-2a-6)=4a2+8a+24=4(a+1)2+20
∵4(a+1)2≥0
∴4(a+1)2+20>0
所以,该函数的图象与x轴总有两个公共点.
(2)①如图1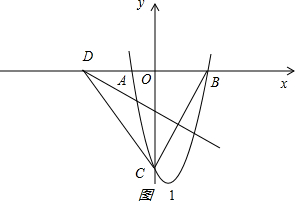 ,
,
把(2,0)代入y=x2-2ax-2a-6得a=1
所以,y=x2-2x-8.
当x=0时,y=-8,即C(0,-8),当y时,x2-2x-8=0,解得x=2(不符合题意,舍),x=4,即B(4,0),
B(4,0)、C(0,-8)
∵点D在BC的垂直平分线上
∴DC=DB
设OD=x,则DC=DB=x+4,
在Rt△ODC中 OD2+OC2=DC2,
即x2+82=(x+4)2,
解得x=6
所以D(-6,0)
②Q1(
,-
)、Q2(10,-8)、Q3(-
,
)、Q4(
,-
).
设BC的中点为E,则点E (2,-4),
直线l的函数关系式为y=-
x-3,
以点B、D、P、Q为顶点的四边形分以下两种情况讨论
第一种情况:当DB为四边形的边时,如图2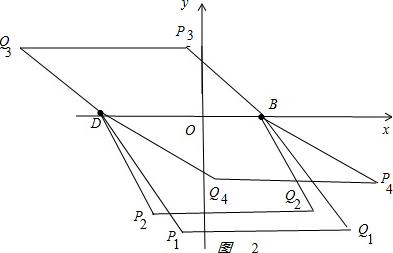 ,
,
当PQ∥DB且PQ=DB时,四边形DPQB为平行四边形,
若PQ在x轴下方时,设点Q(m,-
m-3)则P(m-10,-
m-3),
因为点P在抛物线上,所以-
m-3=(m-10)2-2(m-10)-8.
解得m1=
,m2=10
所以Q1(
,-
)、Q2(10,-8)
若PQ在x轴上方时,设点Q(m,-
m-3)则P(m+10,-
m-3)
因为点P在抛物线上,所以-
m-3=(m+10)2-2(m+10)-8.
解得m1=-
,m2=-6(舍去)
所以Q3(-
,
)
第二种情况:当DB为四边形的对角线时
当DQ4∥PB且DQ4=PB时,四边形D Q4BP为平行四边形
此时可发现DQ4=PB=DQ3,即D为Q3Q4的中点
所以,可求出Q4点(
,-
).
当a≠0时,(-2a)2-4(-2a-6)=4a2+8a+24=4(a+1)2+20
∵4(a+1)2≥0
∴4(a+1)2+20>0
所以,该函数的图象与x轴总有两个公共点.
(2)①如图1
 ,
,把(2,0)代入y=x2-2ax-2a-6得a=1
所以,y=x2-2x-8.
当x=0时,y=-8,即C(0,-8),当y时,x2-2x-8=0,解得x=2(不符合题意,舍),x=4,即B(4,0),
B(4,0)、C(0,-8)
∵点D在BC的垂直平分线上
∴DC=DB
设OD=x,则DC=DB=x+4,
在Rt△ODC中 OD2+OC2=DC2,
即x2+82=(x+4)2,
解得x=6
所以D(-6,0)
②Q1(
| 23 |
| 2 |
| 35 |
| 4 |
| 25 |
| 2 |
| 13 |
| 4 |
| 1 |
| 2 |
| 13 |
| 4 |
设BC的中点为E,则点E (2,-4),
直线l的函数关系式为y=-
| 1 |
| 2 |
以点B、D、P、Q为顶点的四边形分以下两种情况讨论
第一种情况:当DB为四边形的边时,如图2
 ,
,当PQ∥DB且PQ=DB时,四边形DPQB为平行四边形,
若PQ在x轴下方时,设点Q(m,-
| 1 |
| 2 |
| 1 |
| 2 |
因为点P在抛物线上,所以-
| 1 |
| 2 |
解得m1=
| 23 |
| 2 |
所以Q1(
| 23 |
| 2 |
| 35 |
| 4 |
若PQ在x轴上方时,设点Q(m,-
| 1 |
| 2 |
| 1 |
| 2 |
因为点P在抛物线上,所以-
| 1 |
| 2 |
解得m1=-
| 25 |
| 2 |
所以Q3(-
| 25 |
| 2 |
| 13 |
| 4 |
第二种情况:当DB为四边形的对角线时
当DQ4∥PB且DQ4=PB时,四边形D Q4BP为平行四边形
此时可发现DQ4=PB=DQ3,即D为Q3Q4的中点
所以,可求出Q4点(
| 1 |
| 2 |
| 13 |
| 4 |
看了已知二次函数y=x2-2ax-...的网友还看了以下:
21.(5分)阅读下列图片,回答问题。材料一材料二(1)材料一的图2与图1相比较,丝绸之路的起点城 2020-05-14 …
《南都繁会卷》《盛世滋生图》《闭关锁国的清王朝周边形势》反映了什么情况图1,图2与图3反映现象的不 2020-06-11 …
如图1是某条公共汽车线路收支差额y与乘客量x的图象(收支差额=车票收入-支出费用).由于目前本条线 2020-06-25 …
已知函数f(x-1)的图像与函数g(x)的图像关于直线y=x对称,且g(1)=2则:A,f(1)= 2020-06-27 …
非选择题(共5小题,30分)21.(5分)阅读下列图片,回答问题。(1)材料一中图2与图1相比较, 2020-07-17 …
图2与图3人物在推翻秦朝的过程中分别起到了怎样的作用 2020-07-28 …
某人行走时,足部突然受到伤害性刺激,迅速抬脚.图1为相关反射弧示意图,图2与图3为图1部分结构放大示 2020-11-25 …
有关水的实验装置如下图所示。(1)图1为简易净水装置,其中活性炭的作用是;图2为简易蒸馏装置,海水分 2020-11-25 …
从对近代历史推动来看,图2与图1对比最重要的不同是()A.太平洋的发现B.美洲的发现C.非洲地图的拓 2020-12-12 …
如图,已知一次函数y=x+2的图像与x轴交于点A,与二次函数y=ax2+bx+c的图像交于y轴上的一 2021-01-11 …