如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF.其中正确的结论是(
如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF.其中正确的结论是( )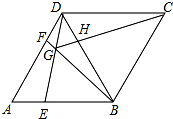
A. 只有①②
B. ①②③
C. 只有②③
D. 只有①③
∴AB=AD.
∵AB=BD,
∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
∴△AED≌△DFB,故本小题正确;
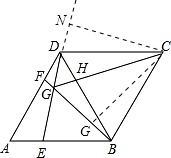
②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,
即∠BGD+∠BCD=180°,
∴点B、C、D、G四点共圆,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°.
∴∠BGC=∠DGC=60°.
过点C作CM⊥GB于M,CN⊥GD于N.
则△CBM≌△CDN,(AAS)
∴S四边形BCDG=S四边形CMGN.
S四边形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM=
| 1 |
| 2 |
| ||
| 2 |
∴S四边形CMGN=2S△CMG=2×
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
③过点F作FP∥AE于P点.
∵AF=2FD,
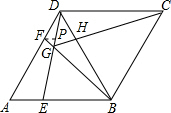
∴FP:AE=DF:DA=1:3,
∵AE=DF,AB=AD,
∴BE=2AE,
∴FP:BE=1:6=FG:BG,
即BG=6GF,故本小题正确.
综上所述,正确的结论有①③.
故选D.
已知f(x)=e^x-e^-x,g(x)=e^x+e^-x(e=2.718……)(1)求【f(x) 2020-05-16 …
两圆相离指外离还是指外离内含同是人教版教科书,初中九年级上册书里讲两圆相离包括外离和内含,现在高中 2020-07-13 …
如图,AB,BC,CD分别于圆O相切于E,F,G,且AB平行于CD,OB于EF相交于M,OC与FG 2020-07-24 …
两圆相离指外离还是指外离内含同是人教版教科书,初中九年级上册书里讲两圆相离包括外离和内含,现在高中 2020-07-26 …
actionscript一次随机选两个不同数一个数组a,b,c,d,e,f,g,h,i,j,我想从 2020-07-27 …
非空集合G关于运算⊕满足:(1)对任意的a,b∈G,都有a⊕b∈G,(2)存在e∈G,都有a⊕e= 2020-08-01 …
相反数问题?下面这道题我不知道该怎么做:推理:(1)由书中知识,+5的相反数是-5,-5的相反数是5 2020-11-06 …
A、B、C、D、E、F、G是中学化学中常见的气体,它们具有如下性质:①A、B、E、F能使湿润的蓝色石 2020-12-02 …
“我们可以得到A和B分别与C、D、E之间的关系”这句话用英语怎么表达“我们可以得到A和B分别与C、D 2020-12-25 …
已知两种分子E和G反应生成另外两种分子L和M(如图),则下列判断正确的是()A.G和M是单质B.L可 2021-01-07 …