下列论述正确的是A.f′（x0）=0是x0为函数f（x）的极值点的充要条件B.是的必要不充分条件C.若f（x）的定义域为R，则f（0）=0是f（x）为奇函数的必要不充分条件D.

Question

下列论述正确的是

1. A.
   f′（x ₀ ）=0是x ₀ 为函数f（x）的极值点的充要条件
2. B.
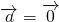   是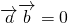 的必要不充分条件
3. C.
   若f（x）的定义域为R，则f（0）=0是f（x）为奇函数的必要不充分条件
4. D.
   若复数z在复平面中对应的点为Z，则z为纯虚数的充要条件为Z在虚轴上

Answer 1

C
分析：
对于A，由极值点的定义判断．对于B，根据向量垂直的定义进行判断；对于C，若函数f（x）的定义域是R，由“f（0）=0”推不出“f（x）为奇函数”．由奇函数的定义可知f（0）=-f（0）所以可得2f（0）=0所以f（0）=0．对于D，利用复平面的特征即可判断正误；

A不正确，点x0为f（x）的极值点由必须满足两个条件一是f′（x0）=0，二是两侧的正负相异．B：∵不能推出，故错；对于C：若函数f（x）的定义域是R，由“f（0）=0”推不出“f（x）为奇函数”．由奇函数的定义可知f（0）=-f（0）所以可得2f（0）=0所以f（0）=0．∴若函数f（x）的定义域是R，则“f（0）=0”是“f（x）为奇函数”的必要不充分条件．正确；对于D：复平面上，除原点外，虚轴上的点都表示纯虚数；故错；故选C．
点评：
本小题主要考查函数在某点取得极值的条件、奇函数的应用、纯虚数的充要条件等基础知识，考查运算求解能力，属于基础题，基本知识掌握不牢固，解答容易出错．