早教吧作业答案频道 -->数学-->
如图,在四棱锥S-ABCD中,底面梯形ABCD中,AD∥BC,平面SAB⊥平面ABCD,△SAB是等边三角形,已知AC=2AB=4,BC=2AD=2CD=25,M是SD上任意一点,SM=mMD,且m>0.(1)求证:平面SAB⊥平面MAC;(2)试确
题目详情
如图,在四棱锥S-ABCD中,底面梯形ABCD中,AD∥BC,平面SAB⊥平面ABCD,△SAB是等边三角形,已知AC=2AB=4,BC=2AD=2CD=2
,M是SD上任意一点,
=m
,且m>0.
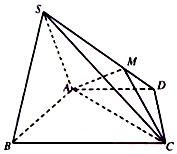
(1)求证:平面SAB⊥平面MAC;
(2)试确定m的值,使三棱锥S-ABC体积为三棱锥S-MAC体积的3倍.
| 5 |
| SM |
| MD |

(1)求证:平面SAB⊥平面MAC;
(2)试确定m的值,使三棱锥S-ABC体积为三棱锥S-MAC体积的3倍.
▼优质解答
答案和解析
(1)证明:在△ABC中,由于AB=2,AC=4,BC=2
,∴AB2+AC2=BC2,故AB⊥AC,
又平面SAB⊥平面ABCD,平面SAB∩平面ABCD=AB,AC⊂平面ABCD,∴AC⊥平面SAB,
又AC⊂平面MAC,
故平面SAB⊥平面MAC;
(2) 在△ACD中,∵AD=CD=
,AC=4,
∴S△ACD=
×4×
=2,
S△ABC=
×2×4=4.
又∵
=m
,
∴VS-MAC=VM-SAC=
•VD-SAC=
•VS-ADC,
∴
=
•
=
•
=
•2=3,
即m=2.
故m的值为2.
| 5 |

又平面SAB⊥平面ABCD,平面SAB∩平面ABCD=AB,AC⊂平面ABCD,∴AC⊥平面SAB,
又AC⊂平面MAC,
故平面SAB⊥平面MAC;
(2) 在△ACD中,∵AD=CD=
| 5 |
∴S△ACD=
| 1 |
| 2 |
(
|
S△ABC=
| 1 |
| 2 |
又∵
| SM |
| MD |
∴VS-MAC=VM-SAC=
| m |
| m+1 |
| m |
| m+1 |
∴
| VS-ABC |
| VS-AMC |
| m+1 |
| m |
| VS-ABC |
| VS-ACD |
| m+1 |
| m |
| S△ABC |
| S△ACD |
| m+1 |
| m |
即m=2.
故m的值为2.
看了如图,在四棱锥S-ABCD中,...的网友还看了以下:
java题java中的接口问题在线等java中1已知类B实现了接口A,设有以下声明Aa;Bb;则以 2020-05-17 …
已知a+b+c=0,试求a^2/(2a^2+bc)+b^2/(2b^2+ac)+c^2/(2c^2 2020-06-12 …
已知:ABC是不在同一条直线上的三点,下列判断正确的是a.AB+AC>BCb.BC+AC>ABc. 2020-07-20 …
如图,下列推理正确的是[]A.∵∠1=∠2(已知)∴AB∥CD(同位角相等,两直线平行)B.∵∠1 2020-07-29 …
如图,△ABC中,∠A=60°,BC为定长,以BC为直径的⊙O分别交AB,AC于点D,E.连接DE 2020-07-31 …
ABC与A'B'C'相似,那么、AB/A'B'=BC/B'C'与BA/A'B'=BC/B'C'有什 2020-08-01 …
用反证法证明命题“已知△A′BC与△ABC有公共边BC,且∠BA′C<∠BAC,求证A′在△ABC 2020-08-01 …
下列各式正确的个数是()(1)x8x4=x2;(2)x2−93−x=x+3;(3)−33x−3=11 2020-10-31 …
已知集合A={直线},B={平面},C=A∪B,若a∈A,b∈B,c∈C,则下列命题中正确的是()A 2020-11-02 …
1、已知a>b>0,比较1/a与1/b的大小.2、下列命题中正确的是:()A、如果ac>bc,则a> 2021-01-04 …