如图1中，∠ABC=90°，点B在直线L上，过A、C两点作直线L的垂线段，垂足分别为点D、点E，容易证得△ADB∽△BEC．此图形如横放的大写英文字母“K”，故常称之为“K形图”，又因为图中的三个

Question

如图1中，∠ABC=90°，点B在直线L上，过A、C两点作直线L的垂线段，垂足分别为点D、点E，容易证得△ADB∽△BEC．此图形如横放的大写英文字母“K”，故常称之为“K形图”，又因为图中的三个直角顶点在同一直线上，又称之为“一线三垂直”，是学习相似三角形的基本图形之一．请以“K形图”为模型，解答下面问题：

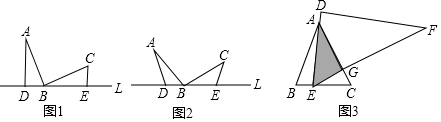
（1）当图1中∠ABC=∠ADB=∠BEC=90°，改为图2中的∠ABC=∠ADB=BEC=α，请问△ADB∽△BEC的结论还成立吗？若成立请证明这个结论，若不成立请说明理由；
（2）如图3，等边△ABC中，AB=6，将一直角三角板DEF的60°角的顶点E置于边BC上移动（不与B、C重合），移动过程中，始终满足直角边DE经过点A，斜边EF交AC于点G．
①求线段AG长度的最小值；
②探究：在点E移动过程中，两三角形重叠部分能否构成等腰三角形？若能，求出此时BE的长，若不能，请说明理由．

Answer 1

（1）结论仍然成立，
理由：根据三角形外角的性质得，∠ABE=∠ABC+∠CBE=∠A+∠ADB，
∵∠ABC=∠ADB=∠BEC=α，
∴∠A=∠CBE，
∵∠ADB=∠BEC，
∴△ADB∽△BEC；
（2）①设BE=x，
∴CE=6-x，
∵∠B=∠AEG=∠C=60°，
由（1）知，△ADB∽△BEC；
∴(CG)/(BE)=(CE)/(AB)，
∴(CG)/(x)=(6-x)/(6)，
∴CG=-(1)/(6)x²+x=-(1)/(6)（x-3）²+(3)/(2)，
当x=3时，CG最长为(3)/(2)；AG最短为6-(3)/(2)=(9)/(2)，
②在点E移动过程中，两三角形重叠部分不能成等腰三角形；
理由：∵∠AEG=60°，如果重叠部分为等腰三角形，则必是等边三角形，
即：AE=EG，
∵△ABE∽△ECG，
那么这两个三角形全等，
则AB=EC，而点E置于边BC上移动不与B，C重合，
∴AB=BC>EC，所以得出矛盾，
即点E移动过程中，两三角形重叠部分不能成等腰三角形．