早教吧作业答案频道 -->数学-->
直角三角形ABC中,∠C=90度,CB=6,AC=8,D为CB边上一个动点,E为AC上一点,DE∥AB,将三角形CDE沿着DE翻折得到三角形DEF,设三角形DEF和三角形ABC重合的面积为y,DC=x,求y与x的函数关系式及定义
题目详情
直角三角形ABC中,∠C=90度,CB=6,AC=8,D为CB边上一个动点,E为AC上一点,DE∥AB,将三角形CDE沿着DE翻折得到三角形DEF,设三角形DEF和三角形ABC重合的面积为y,DC=x,求y与x的函数关系式及定义域.
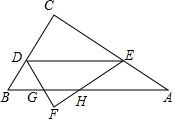

▼优质解答
答案和解析
当0≤x≤3时,点F在△ABC内(包括在边AB上),如图1所示,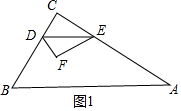
此时△DEF和△ABC重合部分是完整的△DEF.
由翻折的性质可知:△DEF≌△DEC.
∵DE∥AB,
∴
=
,
∴CE=
=
CD=
x,
∴y=
CD•CE=
x2;
当3<x≤6时,点F在△ABC外,如图2所示.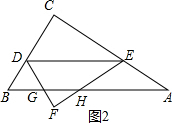
∵DE∥AB,
∴∠CDE=∠B,∠FGH=∠FDE.
由翻折的性质可知:∠CDE=∠FDE,
∴∠B=∠FGH=∠BGD,
∴BD=GD,
∴GF=2x-6,FH=
(2x-6),
∴y=S△CDE-S△FGH=
CD•CE-
GF•FH=-2x2+16x-24.
综上所述:y=
.

此时△DEF和△ABC重合部分是完整的△DEF.
由翻折的性质可知:△DEF≌△DEC.
∵DE∥AB,
∴
| CD |
| CB |
| CE |
| CA |
∴CE=
| CD•CA |
| CB |
| 4 |
| 3 |
| 4 |
| 3 |
∴y=
| 1 |
| 2 |
| 2 |
| 3 |
当3<x≤6时,点F在△ABC外,如图2所示.

∵DE∥AB,
∴∠CDE=∠B,∠FGH=∠FDE.
由翻折的性质可知:∠CDE=∠FDE,
∴∠B=∠FGH=∠BGD,
∴BD=GD,
∴GF=2x-6,FH=
| 4 |
| 3 |
∴y=S△CDE-S△FGH=
| 1 |
| 2 |
| 1 |
| 2 |
综上所述:y=
|
看了 直角三角形ABC中,∠C=9...的网友还看了以下:
谢才系数C与沿程水头损失系数λ的关系是什么A.C与λ成正比B.C与1/λ成正比C.C与λ2成正比D 2020-05-14 …
二项式系数题在(2X-3Y)的十次方的展开式中,求:(1)各项系数的和;(2)含X的奇数次幂项系数 2020-07-27 …
已知(x23+3x2)n的展开式中,各项系数和与它的二项式系数和的比为32.(1)求展开式中二项式 2020-07-27 …
关于展开式的各项系数和与二项式系数之和是不是例如(x+2x)的n次,这样的式子展开式的各项系数和是 2020-07-31 …
某项研究表明:人的眼睛疲劳系数y与睡眠时间t之间成函数关系,它们之间的关系如图2所示.其中,当睡眠 2020-08-02 …
(2x-3y)^10的展开式中求:1.二项式系数和2.各项系数和3.奇数项的二项式系数和偶数项的二 2020-08-03 …
在(2x-3y)10的展开式中,求:(1)各项系数的和;(2)奇数项的二项式系数和与偶数项的二项式 2020-08-03 …
关于展开式的各项系数和与二项式系数之和是不是例如(x+2x)的n次,这样的式子展开式的各项系数和是 2020-08-03 …
关于胡克定律,下列说法中正确的是()A.由F=kx可知,弹力F的大小与弹簧的长度x成正比B.由k=F 2020-11-03 …
某实验小组探究弹簧的劲度系数k与其长度(圈数)的关系实验装置如图(a)所示:一均匀长弹簧的劲度系数k 2020-11-17 …