早教吧作业答案频道 -->物理-->
如图1所示,已知小灯泡L上标有“6V3W”字样,R0=20Ω,滑动变阻器R的最大阻值为100Ω.求:(1)小灯泡的电阻(设灯丝电阻不随温度变化);(2)只闭合S1,移动滑动变阻器滑片P,变阻器
题目详情
如图1所示,已知小灯泡L上标有“6V 3W”字样,R0=20Ω,滑动变阻器R的最大阻值为100Ω.求:
(1)小灯泡的电阻(设灯丝电阻不随温度变化);
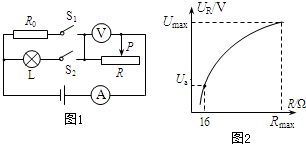
(2)只闭合S1,移动滑动变阻器滑片P,变阻器两端电压与其连入电路的电阻关系如图2所示;当滑片置于某点a时,电压表示数Ua=8V.求此时电流表示数及电源电压;
(3)已知电压表量程为0~15V,在电压表示数不超过量程,灯泡两端电压不超过额定值的情况下,只闭合S2时,求滑动变阻器连入电路的阻值范围.
(1)小灯泡的电阻(设灯丝电阻不随温度变化);
(2)只闭合S1,移动滑动变阻器滑片P,变阻器两端电压与其连入电路的电阻关系如图2所示;当滑片置于某点a时,电压表示数Ua=8V.求此时电流表示数及电源电压;
(3)已知电压表量程为0~15V,在电压表示数不超过量程,灯泡两端电压不超过额定值的情况下,只闭合S2时,求滑动变阻器连入电路的阻值范围.

▼优质解答
答案和解析
(1)由P=
可得,灯泡电阻:
RL=
=
=12Ω;
(2)只闭合S1,R0与R串联,由图2可知,当电压表示数Ua=8V时,R=16Ω,
因串联电路中各处的电流相等,则电路中的电流I=Ia=
=
=0.5A,
总阻值R总=R0+R=20Ω+16Ω=36Ω;
由欧姆定律得:电源电压U=IR总=0.5A×36Ω=18V;
(3)只闭合S2时,灯泡L与变阻器串联,由于灯泡的额定电压为6V,则灯泡两端的电压最大电压为6V;
则由P=UI得电路中的最大电流:I最大=IL=
=
=0.5A,
由欧姆定律得:总电阻R总最小=
=
=36Ω;
由串联电路中总电阻等于各分电阻之和可得:
变阻器接入电路中的最小电阻R最小=R总最小-RL=36Ω-12Ω=24Ω;
为保护电压表的量程,则电压表的最大示数为15V,
由串联电路中总电压等于各分电压之和可得:
灯泡两端的电压为UL′=U-UR最大=18V-15V=3V,
则通过灯泡的最小电流I最小=
=
=0.25A,
由欧姆定律得:变阻器接入电路中的最大电阻R最大=
=
=60Ω;
由此可知:滑动变阻器连入电路的阻值范围是24Ω~60Ω.
答:(1)小灯泡的电阻为12Ω;
(2)电流表示数为0.5A,电源电压为18V;
(3)滑动变阻器连入电路的阻值范围为24Ω~60Ω.
| U2 |
| R |
RL=
| UL2 |
| PL |
| (6V)2 |
| 3W |
(2)只闭合S1,R0与R串联,由图2可知,当电压表示数Ua=8V时,R=16Ω,
因串联电路中各处的电流相等,则电路中的电流I=Ia=
| Ua |
| R |
| 8V |
| 16Ω |
总阻值R总=R0+R=20Ω+16Ω=36Ω;
由欧姆定律得:电源电压U=IR总=0.5A×36Ω=18V;
(3)只闭合S2时,灯泡L与变阻器串联,由于灯泡的额定电压为6V,则灯泡两端的电压最大电压为6V;
则由P=UI得电路中的最大电流:I最大=IL=
| P额 |
| U额 |
| 3W |
| 6V |
由欧姆定律得:总电阻R总最小=
| U |
| I最大 |
| 18V |
| 0.5A |
由串联电路中总电阻等于各分电阻之和可得:
变阻器接入电路中的最小电阻R最小=R总最小-RL=36Ω-12Ω=24Ω;
为保护电压表的量程,则电压表的最大示数为15V,
由串联电路中总电压等于各分电压之和可得:
灯泡两端的电压为UL′=U-UR最大=18V-15V=3V,
则通过灯泡的最小电流I最小=
| UL′ |
| RL |
| 3V |
| 12Ω |
由欧姆定律得:变阻器接入电路中的最大电阻R最大=
| UR最大 |
| I最小 |
| 15V |
| 0.25A |
由此可知:滑动变阻器连入电路的阻值范围是24Ω~60Ω.
答:(1)小灯泡的电阻为12Ω;
(2)电流表示数为0.5A,电源电压为18V;
(3)滑动变阻器连入电路的阻值范围为24Ω~60Ω.
看了如图1所示,已知小灯泡L上标有...的网友还看了以下:
下列判断正确的是()A.只有1的倒数等于它本身B.绝对值小于10的所有整数的和为0C.任何数的相反 2020-05-14 …
50万户居民,平均每户有两个龙头,1%的龙头漏水,每个龙头1秒滴一滴水,10滴约一克,一年要漏掉多 2020-05-14 …
某城市有50万户居民,平均每户有两个水龙头,估计其中有1%的水龙头漏水,每个漏水龙头1秒钟漏一滴水 2020-05-14 …
某城市有50万户居民,平均每户有两个水龙头,估计其中有1%的水龙头漏水,每个漏水龙头1秒钟漏一滴水 2020-05-14 …
数学应用题某城市有59万户居民,平均每户有两个水龙头,估计其中有1%的水龙头漏水,每个漏水龙头1秒 2020-05-14 …
数学概率论:某人买了四节电池,已知这批电池有1%的产品不合格,求着四节电池中恰有1、2、3、4节某 2020-05-15 …
某城市有50万户居民,平均每户有两个水龙头,估计其中有1%的水龙头漏水,每个水龙头每秒钟漏一滴水, 2020-05-17 …
自然光存在着“( ),多种副光,一个投影,光位、光比、光质和色温有变”的自然规律。A.光照强烈B.亮 2020-05-31 …
1到1000这1000个自然数中,完全不含有1的数有多少个? 2020-06-06 …
公约数只有1的两个数,它和除了1以外,没有其他的公约数,是指公约数只有1,没有别的,一样吗?另外除 2020-06-06 …