早教吧作业答案频道 -->数学-->
阅读材料:“最值问题”是数学中的一类较具挑战性的问题.其实,数学史上也有不少相关的故事,如下即为其中较为经典的一则:海伦是古希腊精通数学、物理的学者,相传有位将军曾向
题目详情
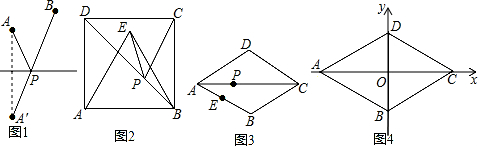
阅读材料:“最值问题”是数学中的一类较具挑战性的问题.其实,数学史上也有不少相关的故事,如下即为其中较为经典的一则:海伦是古希腊精通数学、物理的学者,相传有位将军曾向他请教一个问题--如图1,从A点出发,到笔直的河岸l去饮马,然后再去B地,走什么样的路线最短呢?海伦轻松地给出了答案:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B 的值最小.
解答问题:
(1)如图2,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线BD上有一点P,使PC+PE的和最小,则这个最小值为___.
(2)如图3:菱形ABCD中,AB=2,∠B=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为___.
(3)如图4,已知菱形ABCD的边长为6,∠DAB=60°.将此菱形放置于平面直角坐标系中,各顶点恰好在坐标轴上.现有一动点P从点A出发,以每秒2个单位的速度,沿A→C的方向,向点C运动.当到达点C后,立即以相同的速度返回,返回途中,当运动到x轴上某一点M时,立即以每秒1个单位的速度,沿M→B的方向,向点B运动.当到达点B时,整个运动停止.为使点P能在最短的时间内到达点B处,则点M的坐标是什么?

解答问题:
(1)如图2,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线BD上有一点P,使PC+PE的和最小,则这个最小值为___.
(2)如图3:菱形ABCD中,AB=2,∠B=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为___.
(3)如图4,已知菱形ABCD的边长为6,∠DAB=60°.将此菱形放置于平面直角坐标系中,各顶点恰好在坐标轴上.现有一动点P从点A出发,以每秒2个单位的速度,沿A→C的方向,向点C运动.当到达点C后,立即以相同的速度返回,返回途中,当运动到x轴上某一点M时,立即以每秒1个单位的速度,沿M→B的方向,向点B运动.当到达点B时,整个运动停止.为使点P能在最短的时间内到达点B处,则点M的坐标是什么?
▼优质解答
答案和解析
(1)如图1,
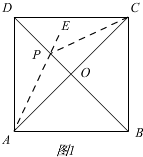
根据正方形的性质可知,
点C关于BD的对称点为点A,
∴PC+PE的和最小值为AE,
∵正方形ABCD的面积为16,
∴AB=4,
∵△ABE是等边三角形,
∴AE=4,
∴PC+PE的和最小值为4;
故答案为4;
(2)如图2
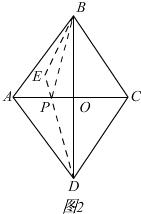
根据菱形的性质可知,
点B关于AC的对称点为点D,
∴DE为PB+PE的最小值,
∵∠B=120°,
∴∠BAD=60°,
∴△ABD是等边三角形,
∵E是AB的中点,所以DE⊥AB,
∵AB=2,∴AE=
,
∴PB+PE的最小值是
;
故答案为
(3)使点P能在最短的时间内到达点B处,
∴当PB⊥AB时,符合题意,
∵∠DAB=60°,
∴∠BAC=30°,又AB=6,
∴BM=2
,
∵∠OBM=30°,BM=2
,
∴OM=
,
∴点M的坐标为(
,0).

根据正方形的性质可知,
点C关于BD的对称点为点A,
∴PC+PE的和最小值为AE,
∵正方形ABCD的面积为16,
∴AB=4,
∵△ABE是等边三角形,
∴AE=4,
∴PC+PE的和最小值为4;
故答案为4;
(2)如图2

根据菱形的性质可知,
点B关于AC的对称点为点D,
∴DE为PB+PE的最小值,
∵∠B=120°,
∴∠BAD=60°,
∴△ABD是等边三角形,
∵E是AB的中点,所以DE⊥AB,
∵AB=2,∴AE=
| 3 |
∴PB+PE的最小值是
| 3 |
故答案为
| 3 |
(3)使点P能在最短的时间内到达点B处,
∴当PB⊥AB时,符合题意,
∵∠DAB=60°,
∴∠BAC=30°,又AB=6,
∴BM=2
| 3 |
∵∠OBM=30°,BM=2
| 3 |
∴OM=
| 3 |
∴点M的坐标为(
| 3 |
看了阅读材料:“最值问题”是数学中...的网友还看了以下:
挖土人数比挑土人数多1/2后来从挖土人调36人到挑土中这时挖土比挑土多1/4求分配前挖土与挑土数各 2020-05-15 …
当两组数据个数相等,平均数相等或接近时,用方差可以比较其波动大小及稳定性,方差较大的数据波动,稳定 2020-06-10 …
微积分的这几本书如何挑选?微积分的好书太多了,如何看呢?是只挑其中1-2本?还是一本一本都看?微积 2020-06-11 …
有四个互不相同的正整数,从中任取两个数且组成一组,并在同一组中用较大的减去较小的数再将各组所得的差 2020-06-15 …
“夹生”用英语怎么讲?这是中国南方的地方话,形容一个人比较挑剔,对人不友善,尤其是初次见面的时候. 2020-06-29 …
用科学记数法表示较大的数或较小的数1.将较大的正数N(N>1)写成a*10n(n是指数)的形式,其 2020-07-03 …
C++编程帮忙挑挑错用穷举法求最大公约数:穷举法求最大公约数方法为:对两个正整数m和n,从r=n( 2020-07-11 …
如何将较大的数分解质因数?较小的数分解质因数很简单,如45=9*550=5*2*5但是如果出现一个 2020-07-31 …
两个数的积是45,其中较小数和较大数的比是1:8,那么较小的数是(),较大数是(). 2020-11-20 …
有两个正数,其中一个比另一个多81,将两数相乘时,算错了,使得乘积的十位数字少了4,再用较大的数去除 2021-01-05 …