早教吧作业答案频道 -->数学-->
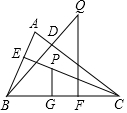
已知:如图,在锐角△ABC中,BD,CE分别是△ABC的AC,AB边上的高,在CE上截取CP=AB,过点P作PG⊥BC于G点,在BD的延长线上截取BQ=AC,过点Q作QF⊥BC于F点,求证:PG+QF=BC.
题目详情
已知:如图,在锐角△ABC中,BD,CE分别是△ABC的AC,AB边上的高,在CE上截取CP=AB,过点P作PG⊥BC于G点,在BD的延长线上截取BQ=AC,过点Q作QF⊥BC于F点,求证:PG+QF=BC.

▼优质解答
答案和解析
证明:如图,作AM⊥BC于M.
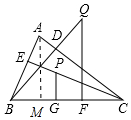
∵CE⊥AB,PG⊥BC,AM⊥BC,
∴∠AMB=∠PGC=∠CEB=90°,
∴∠BAM+∠ABM=90°,∠ABM+∠PCG=90°,
∴∠BAM=∠PCG,
在△PCG和△BAM中,
,
∴△PCG≌△BAM(AAS),
∴PG=BM,
同理可证△BQF≌△ACM,
∴CM=FQ,
∴PG+QF=BM+CM=BC.

∵CE⊥AB,PG⊥BC,AM⊥BC,
∴∠AMB=∠PGC=∠CEB=90°,
∴∠BAM+∠ABM=90°,∠ABM+∠PCG=90°,
∴∠BAM=∠PCG,
在△PCG和△BAM中,
|
∴△PCG≌△BAM(AAS),
∴PG=BM,
同理可证△BQF≌△ACM,
∴CM=FQ,
∴PG+QF=BM+CM=BC.
看了已知:如图,在锐角△ABC中,...的网友还看了以下:
集合A=﹛x|x=3n+1,n∈Z﹜,B=﹛x|x=3n+2,n∈Z﹜,C=﹛x|x=6n+3,n 2020-04-25 …
一元二次方程 -若c(c不等于0)为关于x的一元二次方程x²+bx+c=0的根,则c+b的值为( 2020-05-16 …
下列说法中正确的是()A.乙烯中C=C的键能是乙烷中C-C的键能的2倍B.氮气分子中含有1个σ键和 2020-05-17 …
为什么金刚石中每个碳原子形成四个C-C键金刚石中由共价键构成的最小环有6个碳原子每个环平均拥有:1 2020-06-07 …
1.如是B分之A>0,C分之B>0,那么AC()0;如果B分之A<0,C分之B<0,那么AC()0 2020-07-09 …
cosBcosC-sinBsinC=cos(B+C)为什么cosBcosC-sinBsinC为什么 2020-07-10 …
卷心菜中含有丰富的维生素C,维生素C在酸性溶液中能被碘氧化.某实验小组通过如下实验对卷心菜中维生素C 2020-10-29 …
C/C++谁做了好事一个同学做了件好事,没有留名。A说:不是我。B说:是C。C说:是D。D说:C胡说 2020-11-04 …
①正实数x,y,满足2x+y+6=xy,则求xy的最小值?②正数a,b,c,则a+1/b,b+1/c 2020-11-19 …
已知玉米胚乳有色至少受3对基因控制,一是基本色泽基因C/c,一是紫色基因P/p,P表现紫色,p表现红 2020-11-24 …