早教吧作业答案频道 -->数学-->
如图,E是正方形ABCD的边BC上的一个动点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE,过点F作FG⊥BC交BC的延长线于点G.(1)求证:FG=BE;(2)探索点F是否
题目详情
如图,E是正方形ABCD的边BC上的一个动点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE,过点F作FG⊥BC交BC的延长线于点G.
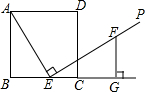
(1)求证:FG=BE;
(2)探索点F是否在∠DCG的平分线上,并说明你的理由.

(1)求证:FG=BE;
(2)探索点F是否在∠DCG的平分线上,并说明你的理由.
▼优质解答
答案和解析
(1)证明:∵EP⊥AE,
∴∠AEB+∠GEF=90°,
又∵∠AEB+∠BAE=90°,
∴∠GEF=∠BAE,
又∵FG⊥BC,
∴∠ABE=∠EGF=90°,
在△ABE与△EGF中,
,
∴△ABE≌△EGF(AAS),
∴FG=BE;
(2) 点F在∠DCG的平分线上,理由如下:
连接CF,如图:
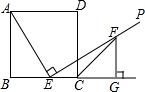
由(1)知:BC=AB=EG,
∴BC-EC=EG-EC,
∴BE=CG,
又∵FG=BE,
∴FG=CG,
又∵∠CGF=90°,
∴∠FCG=45°=
∠DCG,
∴CF平分∠DCG.
∴∠AEB+∠GEF=90°,
又∵∠AEB+∠BAE=90°,
∴∠GEF=∠BAE,
又∵FG⊥BC,
∴∠ABE=∠EGF=90°,
在△ABE与△EGF中,
|
∴△ABE≌△EGF(AAS),
∴FG=BE;
(2) 点F在∠DCG的平分线上,理由如下:
连接CF,如图:

由(1)知:BC=AB=EG,
∴BC-EC=EG-EC,
∴BE=CG,
又∵FG=BE,
∴FG=CG,
又∵∠CGF=90°,
∴∠FCG=45°=
| 1 |
| 2 |
∴CF平分∠DCG.
看了如图,E是正方形ABCD的边B...的网友还看了以下:
能同时与犬.九.工.牙.屈.串组成新字的部首还有 山令川公丁予(与上面不是一题) 2020-05-17 …
已知直径一米,高1.3,求圆柱的侧面面积,是多少个平方,底部与上部不算我要算式跟结果,谢谢!如果加 2020-06-23 …
为了丰富校园文化生活,我们学校英华文学社开展了以“我爱校园”为主题的对联征集活动。请根据所给上联,在 2020-11-02 …
定义:对于抛物线y=ax2+bx+c(a、b、c是常数,a≠0),若b2=ac,则称该抛物线为黄金抛 2020-11-06 …
如图是细胞分裂期的四个时期模式图,下列说法错误的是()A.动物细胞有丝分裂与上图不同之处主要表现在B 2020-11-07 …
奶奶不断唠叨:“老天爷爷,你怎么不睁眼,这雨没完没了地下,你还叫我们穷人活不活。”“奶奶”的话表达了 2020-11-27 …
填上合适的词语1.晶莹的()阴沉的()阴沉的()(要与上面不同)2.填上表示“看”的词语(不重复)( 2020-12-07 …
(1)图是某同学观察后绘制了细胞分裂期的三个时期模式图,请你在下图方框中画出细胞分裂期中所缺时期的模 2021-01-16 …
请问此例子中的justify的意思Investorswillmakeariskyinvestment 2021-01-20 …
数学复数有关问题复数Z满足|z-(1+i)|-|z-(1-i)|=2则复平面内的对应点的轨迹为射线X 2021-01-24 …