已知点A（2，-2）和点B（-4，n）在抛物线y=ax2（a≠0）上．（1）求a的值及点B的坐标；（2）点P在y轴上，且△ABP是以AB为直角边的三角形，求点P的坐标；（3）将抛物线y=ax2（a≠0）向右并向下

Question

已知点A（2，-2）和点B（-4，n）在抛物线y=ax²（a≠0）上．

（1）求a的值及点B的坐标；
（2）点P在y轴上，且△ABP是以AB为直角边的三角形，求点P的坐标；
（3）将抛物线y=ax²（a≠0）向右并向下平移，记平移后点A的对应点为A′，点B的对应点为B′，若四边形ABB′A′为正方形，求此时抛物线的表达式．

Answer 1

（1）把点A（2，-2）代入y=ax²，得到a=-(1)/(2)，
∴抛物线为y=-(1)/(2)x²，
∴x=-4时，y=-8，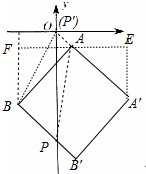
∴点B坐标（-4，-8），
∴a=-(1)/(2)，点B坐标（-4，-8）．
（2）设直线AB为y=kx+b，则有

-4k+b=-8

2k+b=-2

，解得

k=1

b=-4

，
∴直线AB为y=x-4，
∴过点B垂直AB的直线为y=-x-12，与y轴交于点P（0，-12），
过点A垂直AB的直线为y=-x，与y轴交于点P′（0，0），
∴点P在y轴上，且△ABP是以AB为直角边的三角形时．点P坐标为（0，0），或（0，-12）．
（3）如图四边形ABB′A′是正方形，过点A作y轴的垂线，过点B、点A′作x轴的垂线得到点E、F．
∵直线AB解析式为y=-x-12，∴△ABF，△AA′E都是等腰直角三角形，
∵AB=AA′=√(62+62)=6√(2)，
∴AE=A′E=6，
∴点A′坐标为（8，-8），
∴点A到点A′是向右平移6个单位，向下平移6个单位得到，
∴抛物线y=-(1)/(2)x²的顶点（0，0），向右平移6个单位，向下平移6个单位得到（6，-6），
∴此时抛物线为y=-(1)/(2)（x-6）²-6．