早教吧作业答案频道 -->数学-->
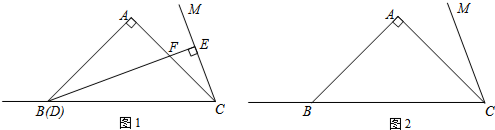
在△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB=45°,在△ABC外侧作∠ACM,使得∠ACM=12∠ABC,点D是射线CB上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.(1)当点D与
题目详情
在△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB=45°,在△ABC外侧作∠ACM,使得∠ACM=
∠ABC,点D是射线CB上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
(1)当点D与点B重合时,如图1所示,线段DF与EC的数量关系是___;
(2)当点D运动到CB延长线上某一点时,线段DF和EC是否保持上述数量关系?请在图2中画出图形,并说明理由.
| 1 |
| 2 |
(1)当点D与点B重合时,如图1所示,线段DF与EC的数量关系是___;
(2)当点D运动到CB延长线上某一点时,线段DF和EC是否保持上述数量关系?请在图2中画出图形,并说明理由.

▼优质解答
答案和解析
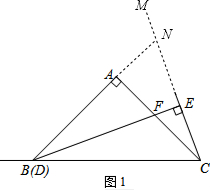 (1)如图1,DF=2EC,理由是:
(1)如图1,DF=2EC,理由是:
延长BA、CM交于点N,
∵∠BAC=∠BEC=90°,∠AFB=∠EFC,
∴∠ABE=∠ACM=
∠ABC,
∴BE平分∠ABC,
∵BE⊥CN,
∴BC=BN,
∴E是CN的中点,
∴NC=2CE,
∵AB=AC,∠BAC=∠CAN=90°,
∴△BAF≌△CAN,
∴BF=CN,
∴BF=2EC,即DF=2EC;
(2)仍然成立,DF=2EC;
理由如下:如图2,作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,
∵DE⊥PC,∠ECD=67.5,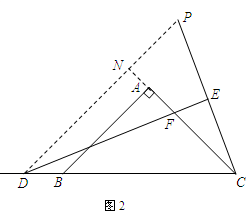
∴∠EDC=22.5°,
∴∠PDE=∠EDC,∠NDC=45°,
∴∠DPC=67.5°,
在△DPE和△DEC中,
,
∴△DPE≌△DEC(AAS),
∴PD=CD,PE=EC,
∴PC=2CE,
∵∠NDC=45°,∠NCD=45°,
∴∠NCD=∠NDC,∠DNC=90°,
∴△NDC是等腰直角三角形
∴ND=NC且∠DNC=∠PNC,
在△DNF和△PNC中,
,
∴△DNF≌△PNC(ASA),
∴DF=PC,
∴DF=2CE.
 (1)如图1,DF=2EC,理由是:
(1)如图1,DF=2EC,理由是:延长BA、CM交于点N,
∵∠BAC=∠BEC=90°,∠AFB=∠EFC,
∴∠ABE=∠ACM=
| 1 |
| 2 |
∴BE平分∠ABC,
∵BE⊥CN,
∴BC=BN,
∴E是CN的中点,
∴NC=2CE,
∵AB=AC,∠BAC=∠CAN=90°,
∴△BAF≌△CAN,
∴BF=CN,
∴BF=2EC,即DF=2EC;
(2)仍然成立,DF=2EC;
理由如下:如图2,作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,
∵DE⊥PC,∠ECD=67.5,

∴∠EDC=22.5°,
∴∠PDE=∠EDC,∠NDC=45°,
∴∠DPC=67.5°,
在△DPE和△DEC中,
|
∴△DPE≌△DEC(AAS),
∴PD=CD,PE=EC,
∴PC=2CE,
∵∠NDC=45°,∠NCD=45°,
∴∠NCD=∠NDC,∠DNC=90°,
∴△NDC是等腰直角三角形
∴ND=NC且∠DNC=∠PNC,
在△DNF和△PNC中,
|
∴△DNF≌△PNC(ASA),
∴DF=PC,
∴DF=2CE.
看了在△ABC中,∠BAC=90°...的网友还看了以下:
1.a≠0,b≠0,则a/|a|+b/|b|的不同取值的个数为()A.3B.2C.1D.02.若|x 2020-03-31 …
数集A满足条件若a∈A则有(1+a)/(1-a)∈A(a≠1)数集A满足条件若a∈A则有(1+a) 2020-04-05 …
基本不等式超费解130已知a>b>0,求a2+1/(a*b)+1/[a*(a-b)]的最小值.a2 2020-05-13 …
线性代数题:设A为n阶方阵,A*是A的伴随矩阵,如果/A/=a≠0,则/A*/=()设A为n阶方阵 2020-05-15 …
设集合A={1,a,b},B={a,a^2,ab}且A=B,求实数A,B的值因为集合需要满足互异性 2020-05-15 …
a-a+1/a=a*a+1/a其中的奥妙是什么?a+1/a是一个数!a-(a+1/a)=a*(a+ 2020-05-16 …
表达变量a中个位,十位,百位数字满足降序关系的正确表达式是A.a%10>a/10%10>a/100 2020-05-17 …
谁能帮我解决一道难题~如题:已知1+a+a*a+a*a*a=0,求a的2008次方+a的2007次 2020-06-10 …
假设集合A满足以下条件:诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …
递回关系式的运算公式(数列)以下是推导一个公式"a=a+r(1-p^n)/(1-p)"的过程a=p* 2021-01-13 …