早教吧作业答案频道 -->数学-->
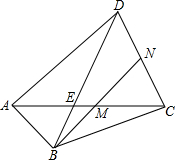
如图,在四边形ABCD中,△ABD,△BCD,△ABC的面积比是3:4:1,点M,N分别在AC,CD上,满足AM:AC=CN:CD,并且B,M,N共线.求证:M与N分别是AC和CD的中点.
题目详情
如图,在四边形ABCD中,△ABD,△BCD,△ABC的面积比是3:4:1,点M,N分别在AC,CD上,满足AM:AC=CN:CD,并且B,M,N共线.求证:M与N分别是AC和CD的中点.

▼优质解答
答案和解析
证明: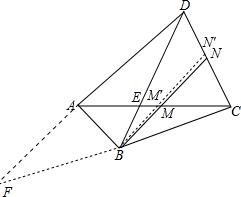 延长DA、CB,交于点F,如图.
延长DA、CB,交于点F,如图.
设S△ABC=S,则,S△ABD=3S,S△BCD=4S.
∵
=
,
=
,
∴
=
,
∴S△AFB=S,
∴S△AFB=S△ABC,
∴FB=BC.
过点B作DF的平行线,交AC于M′,交DC于N′,
根据平行线分线段成比例可得:AM′=CM′,DN′=N′C.
①若点M′在点M的左侧,
则
>
=
,
<
=
,
∴
>
>
,
与条件“AM:AC=CN:CD”矛盾,故舍去;
②若点M′在点M的右侧,
同理可得
<
<
,
与条件“AM:AC=CN:CD”矛盾,故舍去;
③若点M′与点M重合,
则
=
=
,符合条件,
此时M、N分别是AC、DC的中点.
综上所述:M与N分别是AC和CD的中点.
 延长DA、CB,交于点F,如图.
延长DA、CB,交于点F,如图.设S△ABC=S,则,S△ABD=3S,S△BCD=4S.
∵
| S△AFB |
| S△ABC |
| FB |
| BC |
| S△DFB |
| S△DBC |
| FB |
| BC |
∴
| S△AFB |
| S |
| S△AFB+3S |
| 4S |
∴S△AFB=S,
∴S△AFB=S△ABC,
∴FB=BC.
过点B作DF的平行线,交AC于M′,交DC于N′,
根据平行线分线段成比例可得:AM′=CM′,DN′=N′C.
①若点M′在点M的左侧,
则
| AM |
| AC |
| AM |
| AC |
| 1 |
| 2 |
| CN |
| CD |
| CN′ |
| CD |
| 1 |
| 2 |
∴
| AM |
| AC |
| 1 |
| 2 |
| CN |
| CD |
与条件“AM:AC=CN:CD”矛盾,故舍去;
②若点M′在点M的右侧,
同理可得
| AM |
| AC |
| 1 |
| 2 |
| CN |
| CD |
与条件“AM:AC=CN:CD”矛盾,故舍去;
③若点M′与点M重合,
则
| AM |
| AC |
| 1 |
| 2 |
| CN |
| CD |
此时M、N分别是AC、DC的中点.
综上所述:M与N分别是AC和CD的中点.
看了如图,在四边形ABCD中,△A...的网友还看了以下:
f(x),g(x)为[a,b]上的连续函数,证明:存在ξ属于(a,b),使得f(ξ)∫b,ξg(t) 2020-03-30 …
已知b>a>0(1)分式a/b的分子分母都加上1,所得的分式(a+1)/(b+1)的值增大了还是减 2020-06-13 …
如图所示,一个带正电的导体A和一个带负电的导体B用带有绝缘柄的金属杆连接时()A.A球上的部分质子 2020-06-18 …
5道比较简单的大一积分题1.设函数f(x)在[a,b]上具有连续的导函数,且f(a)=f(b)=0 2020-07-28 …
从椭圆a平方分之x^2+b^2分之y^2=1a>b>0上一点p向x轴作垂线垂足恰好为我焦点f1从椭 2020-07-30 …
a的微分乘上b的微分是否等于(a*b)的微分?a的微分加上b的微分是否等于(a+b)的微分? 2020-07-31 …
数学分析问题设f(x)在[a,b]上连续且单增,求证,定积分下界a上界b被积函数xf(x)大于等于 2020-07-31 …
若a>0,b>0a除b>1则a>b若a<0b<0且a除以b<1则a>b以上这种比较大小的方法叫做商 2020-08-01 …
在三角形ABC中,a,b,c分别为角A,B,C所对的边长,且a=3,A=派/3,点D在BC边上.(一 2020-11-02 …
原函数积分加反函数积分…我总不可能画个图吧…怎办…原函数f(x)在[a,b]上单调递增,a>0,f( 2020-11-08 …