早教吧作业答案频道 -->数学-->
在数列an中,,其中n∈N*.(1)求证:数列bn为等差数列;(2)设,试问数列cn中是否存在三项,它们可以构成等差数列?若存在,求出这三项;若不存在,说明理由.(3)已知当n∈N*
题目详情
在数列an中,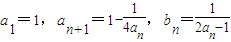 ,其中n∈N*.
,其中n∈N*.
(1)求证:数列bn为等差数列;
(2)设 ,试问数列cn中是否存在三项,它们可以构成等差数列?若存在,求出这三项;若不存在,说明理由.
,试问数列cn中是否存在三项,它们可以构成等差数列?若存在,求出这三项;若不存在,说明理由.
(3)已知当n∈N*且n≥6时,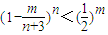 ,其中m=1,2,…n,求满足等式
,其中m=1,2,…n,求满足等式 的所有n的值.
的所有n的值.
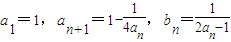 ,其中n∈N*.
,其中n∈N*.(1)求证:数列bn为等差数列;
(2)设
 ,试问数列cn中是否存在三项,它们可以构成等差数列?若存在,求出这三项;若不存在,说明理由.
,试问数列cn中是否存在三项,它们可以构成等差数列?若存在,求出这三项;若不存在,说明理由.(3)已知当n∈N*且n≥6时,
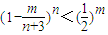 ,其中m=1,2,…n,求满足等式
,其中m=1,2,…n,求满足等式 的所有n的值.
的所有n的值.▼优质解答
答案和解析
【答案】分析:(1)根据等差数列的性质,bn+1-bn为一个常数即可;(2)设,试问数列cn中是否存在三项,它们可以构成等差数列,然后根据等差数列的性质,进行验证;(3)已知当n∈N*且n≥6时,,其中m=1,2,…n,等式进行化简可化为3n+4n++(n+2)n=(n+3)n,然后进行放缩求解;(1)∵∴数列bn为等差数列4;(2)假设数列cn中存在三项,它们可以够成等差数列;不妨设为第p,r,q(p<r<q)项,由(1)得bn=n,∴cn=2n,∴2•2r=2p+2q,∴2r+1-p=1+2q-p又2r+1-p为偶数,1+2q-p为奇数.故不存在这样的三项,满足条件.(3)由(2)得等式可化为3n+4n+…+(n+2)n=(n+3)n即∴∵当n≥6时,,∴,,,∴∴当n≥6时,3n+4n+…+(n+2)n<(n+3)n当n=1,2,3,4,5时,经验算n=2,3时等号成立∴满足等式的所有n=2,3;点评:此题考等差数列的性质,前两问比较简单,第三问难度比较大,放缩时技巧性比较强,不等式与数列的综合题是高考的热点问题,也是压轴题;
看了 在数列an中,,其中n∈N*...的网友还看了以下:
如图,在边长为2的正方形ABCD的一边BC上,一点P从B点运动到C点,设BP=X,四边形APCD的 2020-05-16 …
外星文明是否存在 2020-05-21 …
一种液体饮料采用长方体塑料纸盒密封包装.从外面量盒子长6厘米,宽4厘米,高10厘米.盒面注明“净含 2020-06-20 …
一种液体饮料采用长方体塑料纸盒密封包装,从外面量盒子长6厘米,宽4厘米,高1O厘米.盒面注明“净含 2020-06-30 …
一种液体饮料采用长方体塑封纸盒密封包装.从外面量得纸盒子长6cm,宽4cm,高10cm.盒面注明“ 2020-07-14 …
用数学归纳法证明~~~是否存在常数a,b.使1*n+2(n-1)+3(n-2)+...+(n-2) 2020-08-01 …
一种液体饮料用长方体塑封纸密封包装.从外面量盒子长6厘米,宽4厘米,高10厘米.盒子注明“净含量:2 2020-12-10 …
(2008•龙湖区)一种液体饮料用长方体塑封纸密封包装.从外面量盒子长6厘米,宽4厘米,高10厘米. 2020-12-24 …
关于基因激活的问题比如说B是A的下游靶基因,意思是没有A的激活B就不存在吗?但有些实验中是抑制A,B 2020-12-27 …
教几道题目、、、随便写下过程一种液体饮料采用长方体塑封纸密封包装.从外面量盒子长6CM,宽4CM,高 2021-02-12 …