早教吧作业答案频道 -->数学-->
如图,在RT△ABC中,AC=BC,将△ABC绕点C顺时针旋转45°后得到△DEC,AB与DE相交于点F.(1)试判断DE与AC的位置关系并证明;(2)试探究四边形ACEF是什么特殊的四边形,并证明你的结论;(3
题目详情
如图,在RT△ABC中,AC=BC,将△ABC绕点C顺时针旋转45°后得到△DEC,AB与DE相交于点F.
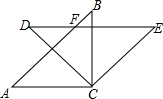
(1)试判断DE与AC的位置关系并证明;
(2)试探究四边形ACEF是什么特殊的四边形,并证明你的结论;
(3)若AC=1,求BF的长.

(1)试判断DE与AC的位置关系并证明;
(2)试探究四边形ACEF是什么特殊的四边形,并证明你的结论;
(3)若AC=1,求BF的长.
▼优质解答
答案和解析
(1)∵在Rt△ABC中,AC=BC,
∴∠A=∠B=45°.
由旋转的性质可知:∠ACD=∠BCE=45°,∠D=∠A=45°.
∴∠D=∠DCA=45°.
∴DE∥AC.
(2)∵∠B=45°,∠BCE=45°,
∴∠B=∠BCE.
∴AB∥CE.
由(1)可知:DE∥AC,
∴四边形ACEF是平行四边形.
又∵AC=CE,
∴四边形ACEF是菱形.
(3)∵四边形ACEF是菱形,
∴AF=AC=1.
在Rt△ABC中,AB=
=
=
.
∴BF=AB-AF=
-1.
∴∠A=∠B=45°.
由旋转的性质可知:∠ACD=∠BCE=45°,∠D=∠A=45°.
∴∠D=∠DCA=45°.
∴DE∥AC.
(2)∵∠B=45°,∠BCE=45°,
∴∠B=∠BCE.
∴AB∥CE.
由(1)可知:DE∥AC,
∴四边形ACEF是平行四边形.
又∵AC=CE,
∴四边形ACEF是菱形.
(3)∵四边形ACEF是菱形,
∴AF=AC=1.
在Rt△ABC中,AB=
| AC2+BC2 |
| 12+12 |
| 2 |
∴BF=AB-AF=
| 2 |
看了如图,在RT△ABC中,AC=...的网友还看了以下:
一质点自原点开始在x轴上运动,初速度v>0,加速度a>0,当加速度a值不断减小至0时,质点的()A 2020-04-05 …
一质点自原点开始在x轴运动,初速度V0>0,加速度a>0,当a值不断减小直到0时,质点的( )A速 2020-04-05 …
一质点自原点开始在x轴上运动,初速度v>0,加速度a>0,当加速度a值不断减小至0时,质点的( ) 2020-04-05 …
计算机一旦发生中断,将进入中断处理,转入操作系统程序的运行。操作系统程序的入口地址出现在(26) 2020-05-26 …
如果库存系统与GSP系统集成使用,必须将本年度与GSP系统相关的库存业务全部完成后,再进行库存系统1 2020-05-31 …
下列关于断层的表述正确的是( )。A.断层系岩体受力作用断裂面产生不大相对位移的断裂B.轻 2020-06-07 …
下列关于断层的表述正确的是( )。 A.断层系岩体受力作用断裂面产生不大相对位移的断 2020-06-07 …
2006年8月24日国际天文学联合会通过新的行星定义,将地位备受争议的冥王星“开出”出太阳系行星行列 2020-11-20 …
关于化学平衡的麻烦举个例子,第一个例子:在生产中,也可以不断将生成物从反应体系中分离出来,则平衡将不 2020-12-25 …
关于化学平衡的麻烦举个例子,第一个例子:在生产中,也可以不断将生成物从反应体系中分离出来,则平衡将不 2020-12-25 …