如图，在▱ABCD中，对角线AC、BD相交于点O，点E、F是AD上的点，且AE=EF=FD．连接BE、BF，使它们分别与AO相交于点G、H．（1）求EG

Question

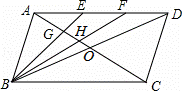
  如图，在 ▱ABCD 中，对角线 AC 、 BD 相交于点 O ，点 E 、 F 是 AD 上的点，且 AE=EF=FD ．连接 BE 、 BF ，使它们分别与 AO 相交于点 G 、 H ．

（ 1 ）求 EG ： BG 的值；

（ 2 ）求证： AG=OG ；

（ 3 ）设 AG=a ， GH=b ， HO=c ，求 a ： b ： c 的值．

Answer 1

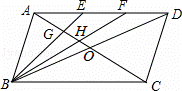
（ 1 ） ∵ 四边形 ABCD 是平行四边形，

∴AO= AC ， AD=BC ， AD∥BC ，

∴△AEG∽△CBG ，

∴ = = ．

∵AE=EF=FD ，

∴BC=AD=3AE ，

∴GC=3AG ， GB=3EG ，

∴EG ： BG=1 ： 3 ；

（ 2 ） ∵GC=3AG （已证），

∴AC=4AG ，

∴AO= AC=2AG ，

∴GO=AO ﹣ AG=AG ；

（ 3 ） ∵AE=EF=FD ，

∴BC=AD=3AE ， AF=2AE ．

∵AD∥BC ，

∴△AFH∽△CBH ，

∴ = = = ，

∴ = ，即 AH= AC ．

∵AC=4AG ，

∴a=AG= AC ，

b=AH ﹣ AG= AC ﹣ AC= AC ，

c=AO ﹣ AH= AC ﹣ AC= AC ，

∴a ： b ： c= ： ： =5 ： 3 ： 2 ．