如图，有足够多的边长为a的小正方形（A类），长为b宽为a的长方形（B类）以及边长为b的大正方形（C类），发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式，比如图②

Question

如图，有足够多的边长为a的小正方形（A类），长为b宽为a的长方形（B类）以及边长为b的大正方形（C类）
，发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式，比如图②可以解释为：（a+2b）（a+b）=a²+3ab+2b²

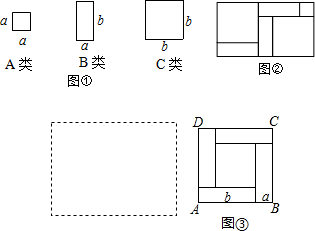
（1）取图①中的若干个（三种图形都要取到）拼成一个长方形，使其面积为（2a+b）（a+2b），在下面虚框中画出图形，并根据图形回答（2a+b）（a+2b）=___．
（2）若取其中的若干个（三种图形都要取到）拼成一个长方形，使其面积为a²+5ab+6b²．
①你画的图中需C类卡片___张．
②可将多项式a²+5ab+6b²分解因式为___
（3）如图③，大正方形的边长为m，小正方形的边长为n，若用x、y表示四个相同矩形的两边长（x>y），观察图案并判断，将正确关系式的序号填写在横线上___（填写序号）
①xy= (m2-n2)/(4)　②x+y=m　　　③x²-y²=m•n　　　　　④x²+y²= (m2+n2)/(2)．

Answer 1

（1）（2a+b）（a+2b）=2a²+5ab+2b²，
故答案为：2a²+5ab+2b²；

（2）①∵长方形的面积为a²+5ab+6b²，
∴画的图中需要C类卡片6张，
故答案为：6．

②a²+5ab+6b²=（a+2b）（a+3b），
故答案为：（a+2b）（a+3b）．

（3） 根据图③得：x+y=m，
∵m²-n²=4xy，
∴xy=(m2-n2)/(4)，
x²-y²=（x+y）（x-y）=mn，
∴x²+y²=（x+y）²-2xy=m²-2×(m2-n2)/(4)=(m2+n2)/(2)．
∴选项①②③④都正确．
故答案为：①②③④．