已知定义在R上的奇函数f（x）满足f（x+2）=-f（x-2），且在区间[0，2]上是减函数．若方程f（x）=m（m>0）在区间[-8，8]上有四个不同的根x1，x2，x3，x4，则x1+x2+x3+x4=（）A.-8B.8C.4D.-4

Question

已知定义在R上的奇函数f（x）满足f（x+2）=-f（x-2），且在区间[0，2]上是减函数．若方程f（x）=m（m>0）在区间[-8，8]上有四个不同的根x₁，x₂，x₃，x₄，则x₁+x₂+x₃+x₄=（　　）

A. -8

B. 8

C. 4

D. -4

Answer 1

∵f（x+2）=-f（x-2）
∴f（x+4）=-f（x）
∴f（x+8）=-f（x+4）
即 f（x）=f（x+8）
∴f（x）是一个周期函数，周期为8，
又函数是奇函数，所以f（x）关于原点对称．
由f（x）在[0，2]上是减函数，可做函数图象示意图如图：

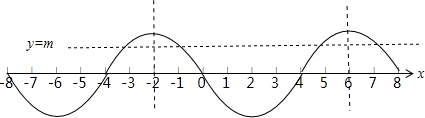
设x₁234，
∵f（x）关于y轴对称，结合周期性知，函数关于x=4对称
∴x₁+x₂=-4^_且x₃+x₄=12，
∴x₁+x₂+x₃+x₄=8，
故选：B．