早教吧作业答案频道 -->数学-->
在正方体ABCD-A1B1C1D1中E,G,H分别为BC,C1D1,AA1的中点.(1)求证:EG∥平面BDD1B1;(2)求异面直线B1H与EG所成的角.
题目详情
在正方体ABCD-A1B1C1D1中E,G,H分别为BC,C1D1,AA1的中点.
( 1)求证:EG∥平面BDD1B1;
( 2)求异面直线B1H与 EG所成的角.
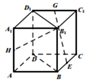
( 1)求证:EG∥平面BDD1B1;
( 2)求异面直线B1H与 EG所成的角.

▼优质解答
答案和解析
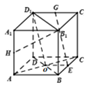 (1)证明:ABCD-A1B1C1D1是正方体,E,G,H分别为BC,C1D1,AA1的中点,
(1)证明:ABCD-A1B1C1D1是正方体,E,G,H分别为BC,C1D1,AA1的中点,
连结AC交BD于O连结DO,OE,
∵OE
CD,OD
D1G
∴四边形OEGD1为平行四边形
∴EG∥OD1,又EG⊄面BDD1B1,OD1⊂面BDD1B1,
∴EG∥平面BDD1B1.
(2)延长DB于M,使BM=
BD,
连结B1M,HM,∠HB1M为所求角.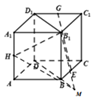
设正方体边长为1,则B1M=
,B1H=
,AM=
,HM=
,
∴cos∠HB1M=0,
∴B1H与EG所成的角为90°.
 (1)证明:ABCD-A1B1C1D1是正方体,E,G,H分别为BC,C1D1,AA1的中点,
(1)证明:ABCD-A1B1C1D1是正方体,E,G,H分别为BC,C1D1,AA1的中点,连结AC交BD于O连结DO,OE,
∵OE
| ||
. |
| 1 |
| 2 |
| ||
. |
∴四边形OEGD1为平行四边形
∴EG∥OD1,又EG⊄面BDD1B1,OD1⊂面BDD1B1,
∴EG∥平面BDD1B1.
(2)延长DB于M,使BM=
| 1 |
| 2 |
连结B1M,HM,∠HB1M为所求角.

设正方体边长为1,则B1M=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴cos∠HB1M=0,
∴B1H与EG所成的角为90°.
看了 在正方体ABCD-A1B1C...的网友还看了以下:
德布罗意波长公式求教注:v频率E=hνv=c/λ所以E=hc/λh/λ=E/cp=hν/cc=vλ 2020-06-22 …
这5道题用波兰式表达(1)A*(B-C)+T/(D+E)-F/(S*H)(2)A/(B*C(E+F 2020-07-08 …
一个9位数abcdefghi满足:1.a+b+...+h+i=cd2.a(b+d-c)=243.( 2020-07-19 …
三元一次方程组a*x+b*y+c*z+d=0,e*x+f*y+g*z+h=0,i*x+j*y+k* 2020-08-03 …
该地质演化过程的正确排序是()A.d-e-g-f-b-a-h-cB.d-g-e-a-c-h-b-fC 2020-11-04 …
一个9位数abcdefghi满足:1.a+b+...+h+i=cd2.a(b+d-c)=243.(e 2020-11-19 …
已知AB是圆O的直径,C,E是圆上的点,CD垂直AB,EF垂直AB垂足分别为D,F过E作EG垂直OC 2020-11-27 …
n.h.c.e.r.t这六个单词能组成什么单词?急!应该是:n.h.c.e.r.t这六个单词合在一起 2020-11-27 …
英语:下1.将下联打乱的字母组成单词,并写出汉语意思1.a,e,h,g,c,n[]2.e,i,s,t 2020-12-10 …
A+B+C=84,D+E+F=111,H+I+J=138,A+D+H=124,B+E+I=148,C 2020-12-14 …