早教吧作业答案频道 -->数学-->
如图,在三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,倒棱AA1⊥平面ABC,点E,F分别是棱CC1,BB1上的点,且EC=2FB=2.(Ⅰ)若点M是线段AC的中点,证明:(1)MB∥平面AEF;(2)平面AEF⊥平
题目详情
如图,在三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,倒棱AA1⊥平面ABC,点E,F分别是棱CC1,BB1上的点,且EC=2FB=2.
(Ⅰ)若点M是线段AC的中点,证明:
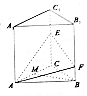
(1)MB∥平面AEF;
(2)平面AEF⊥平面ACC1A1;
(Ⅱ)求三棱锥B-AEF的体积.
(Ⅰ)若点M是线段AC的中点,证明:

(1)MB∥平面AEF;
(2)平面AEF⊥平面ACC1A1;
(Ⅱ)求三棱锥B-AEF的体积.
▼优质解答
答案和解析
(Ⅰ)证明:(1)取线段AE的中点G,连结MG,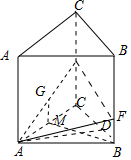
则MG=
EC=BF,又MG∥EC∥BF,
∴MBFG是平行四边形,故MB∥FG.
而FG⊂平面AEF,MB⊄平面AEF,
∴MB∥平面AEF;
(2)∵MB⊥AC,平面ACC1A1⊥平面ABC,
∴MB⊥平面ACC1A1,而BM∥FG,
∴FG⊥平面ACC1A1.
∵FG⊂平面AEF,∴平面AEF⊥平面ACC1A1;
(Ⅱ) 作AD⊥BC于D,则AD⊥平面BEF,且AD=
.
于是VA-BEF=
×S△BEF×AD=
×
×1×2×
=
.
故VB-AEF=VA-BEF=
.

则MG=
| 1 |
| 2 |
∴MBFG是平行四边形,故MB∥FG.
而FG⊂平面AEF,MB⊄平面AEF,
∴MB∥平面AEF;
(2)∵MB⊥AC,平面ACC1A1⊥平面ABC,
∴MB⊥平面ACC1A1,而BM∥FG,
∴FG⊥平面ACC1A1.
∵FG⊂平面AEF,∴平面AEF⊥平面ACC1A1;
(Ⅱ) 作AD⊥BC于D,则AD⊥平面BEF,且AD=
| 3 |
于是VA-BEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
故VB-AEF=VA-BEF=
| ||
| 3 |
看了 如图,在三棱柱ABC-A1B...的网友还看了以下:
由1-9九位数字组成的三个随机数字,其比例是1:2:3用c#将1到9共9个数分为三组,组成3个三位 2020-04-07 …
关于一三是‘如’的词语比如:如泣如诉、如火如荼、如痴如醉. 2020-05-13 …
如果存款利率如下所示存期一年两年三年利率2.25%2.48%2.70%王华有20000元整存入银行 2020-05-13 …
有关可解(无复数根)一元三次方程类型如(假设)X^3-7X^2+12X-9=0试根1,2,3,-1 2020-05-14 …
第一字是第四声,第2字是第三声,第三是第2声,第四是第一声的成语有哪些 2020-05-15 …
如图所示,ABCD是菱形,对角线AC与BD相交于点O,角ACD=30°,BD=6.(1)求证:三角 2020-05-16 …
利用球面坐标计算三重积分时的ψ是如何确定啊比如:∫∫∫(x^2+y^2+z^2)dv,其中Ω是由球 2020-06-14 …
利用球面坐标计算三重积分时的ψ是如何确定啊比如:∫∫∫(x^2+y^2+z^2)dv,其中Ω是由球 2020-06-14 …
2一个长方形的长与宽的比是6比5,如果长是三十厘米,那么宽是,如果周长是三十厘米,那么长十几厘米一 2020-07-17 …
规定一种新的运算:a三角形b等于a乘b减a加1,如3三角形4等于3乘4减3加1,请比较-3三角形2 2020-07-20 …