早教吧作业答案频道 -->数学-->
已知:如图,在四边形ABCD中,P、Q、M、N分别是AD、BC、BD、AC的中点.(1)求证:PQ、MN互相平分;(2)当四边形ABCD的边满足条件:时,PQ⊥MN.(不必证明)
题目详情
已知:如图,在四边形ABCD中,P、Q、M、N分别是AD、BC、BD、AC的中点.
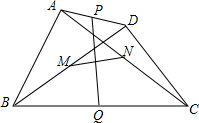
(1)求证:PQ、MN互相平分;
(2)当四边形ABCD的边满足条件:___时,PQ⊥MN.(不必证明)

(1)求证:PQ、MN互相平分;
(2)当四边形ABCD的边满足条件:___时,PQ⊥MN.(不必证明)
▼优质解答
答案和解析
(1)证明:连接MP、NP、MQ、NQ,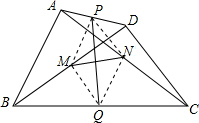
∵P、M分别是AD、BD的中点,
∴PM=
AB,PM∥AB,
同理NQ=
AB,NQ∥AB,
∴PM∥NQ,PM=NQ,
∴四边形PMQN是平行四边形,
∴PQ、MN互相平分;
(2)AB=CD,
∵PM=
AB,PN=
CD,
当AB=CD时,PM=PN,
则平行四边形PMQN是菱形,
∴PQ⊥MN.

∵P、M分别是AD、BD的中点,
∴PM=
| 1 |
| 2 |
同理NQ=
| 1 |
| 2 |
∴PM∥NQ,PM=NQ,
∴四边形PMQN是平行四边形,
∴PQ、MN互相平分;
(2)AB=CD,
∵PM=
| 1 |
| 2 |
| 1 |
| 2 |
当AB=CD时,PM=PN,
则平行四边形PMQN是菱形,
∴PQ⊥MN.
看了 已知:如图,在四边形ABCD...的网友还看了以下:
大学数学关于柯西列的问题证明a(n)=∑(sink/2^k)k=1,2.n,是柯西列.我考虑sin 2020-04-26 …
高等代数的一个符号?sl(n,P)={A}中的sl表示什么意思?是有限群的意思吗? 2020-05-13 …
答案是不是21?#includestructS{inta,b;}data[2]={10,100,2 2020-05-17 …
速度前n项和sn=3^(n-1)+a当a=时数列an为等比数列 2020-05-22 …
VBA代码中看见Dimm%,n%,p%,a,这句中的a是什么意思,为何这样写? 2020-07-19 …
高手多元二次方程是否可解,(Am+Bn+Cp)x+(Ca+Db)y=Mx+y=1;m+n+p=1; 2020-08-02 …
求下列极限lim(n→∞)(n^p)/(a^n)(p>0a>0) 2020-11-01 …
随机事件A发生的概率P(A)的范围是;当A是必然事件时,p(A),当A是不可能事件时,P(A). 2020-11-03 …
1、已知:a、b互为相反数,x、y互为倒数,|m|=1,求m的平方-2(a+b+xy)+(a+b)的 2020-11-03 …
在资金时间价值计算时,i和n给定,下列等式中正确的有().A.(F/A,i,n)=[(P/F,i,n 2021-01-14 …