早教吧作业答案频道 -->数学-->
如图,已知二次函数y=-x2-2x+3的图象交x轴于A、B两点(A在B左边),交y轴于C点.(1)求A、B、C三点的坐标和直线AC的解析式;(2)点P是直线AC上方抛物线上一动点(不与A,C重合),过点P作
题目详情
如图,已知二次函数y=-x2-2x+3的图象交x轴于A、B两点(A在B左边),交y轴于C点.
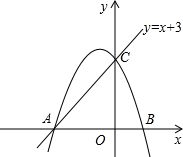
(1)求A、B、C三点的坐标和直线AC的解析式;
(2)点P是直线AC上方抛物线上一动点(不与A,C重合),过点P作x轴平行线交直线AC于M点,求线段PM的最大值.

(1)求A、B、C三点的坐标和直线AC的解析式;
(2)点P是直线AC上方抛物线上一动点(不与A,C重合),过点P作x轴平行线交直线AC于M点,求线段PM的最大值.
▼优质解答
答案和解析
(1)令y=0,得:-x2-2x+3=0,解得:x1=-3,x2=1,
∴点A(-3,0),点B(1,0);
令x=0,得:y=3,
∴点C(0,3);
设直线AC的解析式为:y=kx+b,点A(-3,0),点C(0,3)在直线AC上,
,解得:
,
∴直线AC的解析式为:y=x+3.
(2)如图所示,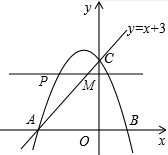
设点P的坐标为(a,-a2-2a+3),
由PM∥x轴,可知点M的纵坐标为-a2-2a+3,
∴x+3=-a2-2a+3,
∴x=-a2-2a,
∴PM=-a2-2a-a=-a2-3a(-3<a<0),
当a=-
=-
=-
时,PM最大=
.
∴点A(-3,0),点B(1,0);
令x=0,得:y=3,
∴点C(0,3);
设直线AC的解析式为:y=kx+b,点A(-3,0),点C(0,3)在直线AC上,
|
|
∴直线AC的解析式为:y=x+3.
(2)如图所示,
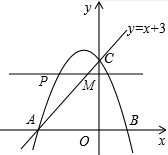
设点P的坐标为(a,-a2-2a+3),
由PM∥x轴,可知点M的纵坐标为-a2-2a+3,
∴x+3=-a2-2a+3,
∴x=-a2-2a,
∴PM=-a2-2a-a=-a2-3a(-3<a<0),
当a=-
| b |
| 2a |
| -3 |
| -2 |
| 3 |
| 2 |
| 9 |
| 4 |
看了 如图,已知二次函数y=-x2...的网友还看了以下:
大小两数的合于差相乘积是四十分之九,两数的合是一又二分之一,求大小两数是多少?最好用算术,如用方程 2020-04-27 …
已知二次函数..已知二次函数y=-1/2x^+(n+1/2)x+n+1,它的图像与x轴交于点A(x 2020-05-13 …
有关不定积分的一个问题问题是这样的:已知速度函数v(t)=t^2[速度等于时间的平方],根据速度函 2020-05-14 …
一道函数题,关键就是奇函数的对称问题,已知函数f(x)是定义在R上的奇函数,且她的图像关于直线x= 2020-05-16 …
函数关于x、y轴对称一次函数y=kx+b二次函数y=ax^2+bx+c关于x轴、y轴对称,这些常数 2020-05-16 …
关于三角函数合一变形的问题(答好一定加分)y=asinx+bcosx则y=√a^2+b^2sin( 2020-06-02 …
已知一次函数与反比例函数交于点P(-2,1)和Q(1,m)(1)求这个函数的关系式(2)在同一坐标 2020-06-04 …
函数与其自己的反函数复合后等于x,怎么证明呢?假设f是g的反函数,于是对定义域内的x,存在y使得, 2020-06-08 …
关于偶函数对于偶函数,有一点我觉得很迷惑啊.大家都知奇函数f(x)=f(-x),但是如果f(x+2 2020-06-09 …
关于奇函数的问题,已知f(x+1)是定义域在R上的奇函数,则f(x+1)的对称中心是什么?f(x) 2020-06-09 …