早教吧作业答案频道 -->数学-->
已知直线y=mx+4与反比例函数y=kx(k<0)的图象交于A,B两点,与x轴,y轴分别交于点C,D,OD=2OC,点A的纵坐标为6.(1)求反比例函数的表达式;(2)若点P(a,b)在线段AC上,过点P作x轴的
题目详情
已知直线y=mx+4与反比例函数y=
(k<0)的图象交于A,B两点,与x轴,y轴分别交于点C,D,OD=2OC,点A的纵坐标为6.
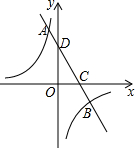
(1)求反比例函数的表达式;
(2)若点P(a,b)在线段AC上,过点P作x轴的平行线与反比例函数图象交于点E,当△PCE的面积为3时,求a的值;
(3)点M在直线x=1上,点N在反比例函数的图象上,当以A,B,M,N为顶点的四边形是平行四边形,求点N的坐标.已知直线y=mx+4与反比例函数y=
(k<0)的图象交于A,B两点,与x轴,y轴分别交于点C,D,OD=2OC,点A的纵坐标为6.

(1)求反比例函数的表达式;
(2)若点P(a,b)在线段AC上,过点P作x轴的平行线与反比例函数图象交于点E,当△PCE的面积为3时,求a的值;
(3)点M在直线x=1上,点N在反比例函数的图象上,当以A,B,M,N为顶点的四边形是平行四边形,求点N的坐标.
(k<0)的图象交于A,B两点,与x轴,y轴分别交于点C,D,OD=2OC,点A的纵坐标为6.

(1)求反比例函数的表达式;
(2)若点P(a,b)在线段AC上,过点P作x轴的平行线与反比例函数图象交于点E,当△PCE的面积为3时,求a的值;
(3)点M在直线x=1上,点N在反比例函数的图象上,当以A,B,M,N为顶点的四边形是平行四边形,求点N的坐标.
k x k k x x

| k |
| x |

(1)求反比例函数的表达式;
(2)若点P(a,b)在线段AC上,过点P作x轴的平行线与反比例函数图象交于点E,当△PCE的面积为3时,求a的值;
(3)点M在直线x=1上,点N在反比例函数的图象上,当以A,B,M,N为顶点的四边形是平行四边形,求点N的坐标.已知直线y=mx+4与反比例函数y=
| k |
| x |

(1)求反比例函数的表达式;
(2)若点P(a,b)在线段AC上,过点P作x轴的平行线与反比例函数图象交于点E,当△PCE的面积为3时,求a的值;
(3)点M在直线x=1上,点N在反比例函数的图象上,当以A,B,M,N为顶点的四边形是平行四边形,求点N的坐标.
| k |
| x |

(1)求反比例函数的表达式;
(2)若点P(a,b)在线段AC上,过点P作x轴的平行线与反比例函数图象交于点E,当△PCE的面积为3时,求a的值;
(3)点M在直线x=1上,点N在反比例函数的图象上,当以A,B,M,N为顶点的四边形是平行四边形,求点N的坐标.
| k |
| x |

▼优质解答
答案和解析
(1)由题意D(0,4),
∴OD=4,
∵OD=2OC,
∴OC=2,
∴C(2,0),
把C(2,0)代入y=mx+4,得到2m+4=0,
∴m=-2,
∴直线的解析式为y=-2x+4,
当y=6时,6=-2x+4,
∴x=-1,
∴A(-1,6),
∴k=-6,
∴反比例函数的解析式为y=-
.
(2)如图,PE∥OC,

∵P(a,b),
∴E(-
,b),
∴PE=a+
,
由题意
•(a+
)•b=3 ①
∵b=-2a+4 ②
由①②得到
,
∴a=0.
(3)作AK∥x轴,BK∥y轴交AK于K.作N2H⊥直线x=1于H.
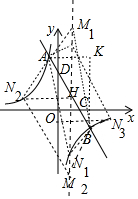
由
解得
或
,
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
的交点N1(1,-6),这个点N1即为所求.
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
),
综上所述,满足条件的点N的坐标为(1,-6)
6 x 6 6 6x x x.
(2)如图,PE∥OC,

∵P(a,b),
∴E(-
,b),
∴PE=a+
,
由题意
•(a+
)•b=3 ①
∵b=-2a+4 ②
由①②得到
,
∴a=0.
(3)作AK∥x轴,BK∥y轴交AK于K.作N2H⊥直线x=1于H.

由
解得
或
,
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
的交点N1(1,-6),这个点N1即为所求.
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
),
综上所述,满足条件的点N的坐标为(1,-6)
6 b 6 6 6b b b,b),
∴PE=a+
,
由题意
•(a+
)•b=3 ①
∵b=-2a+4 ②
由①②得到
,
∴a=0.
(3)作AK∥x轴,BK∥y轴交AK于K.作N2H⊥直线x=1于H.

由
解得
或
,
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
的交点N1(1,-6),这个点N1即为所求.
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
),
综上所述,满足条件的点N的坐标为(1,-6)
6 b 6 6 6b b b,
由题意
•(a+
)•b=3 ①
∵b=-2a+4 ②
由①②得到
,
∴a=0.
(3)作AK∥x轴,BK∥y轴交AK于K.作N2H⊥直线x=1于H.

由
解得
或
,
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
的交点N1(1,-6),这个点N1即为所求.
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
),
综上所述,满足条件的点N的坐标为(1,-6)
1 2 1 1 12 2 2•(a+
)•b=3 ①
∵b=-2a+4 ②
由①②得到
,
∴a=0.
(3)作AK∥x轴,BK∥y轴交AK于K.作N2H⊥直线x=1于H.

由
解得
或
,
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
的交点N1(1,-6),这个点N1即为所求.
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
),
综上所述,满足条件的点N的坐标为(1,-6)
6 b 6 6 6b b b)•b=3 ①
∵b=-2a+4 ②
由①②得到
,
∴a=0.
(3)作AK∥x轴,BK∥y轴交AK于K.作N2H⊥直线x=1于H.

由
解得
或
,
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
的交点N1(1,-6),这个点N1即为所求.
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
),
综上所述,满足条件的点N的坐标为(1,-6)
a=0 b=4 a=0 a=0 a=0b=4 b=4 b=4
∴a=0.
(3)作AK∥x轴,BK∥y轴交AK于K.作N22H⊥直线x=1于H.

由
解得
或
,
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
的交点N1(1,-6),这个点N1即为所求.
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
),
综上所述,满足条件的点N的坐标为(1,-6)
y=-
y=-2x+4 y=-
y=-
y=-
6 x 6 6 6x x xy=-2x+4 y=-2x+4 y=-2x+4
或
,
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
的交点N1(1,-6),这个点N1即为所求.
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
),
综上所述,满足条件的点N的坐标为(1,-6)
x=-1 y=4 x=-1 x=-1 x=-1y=4 y=4 y=4
,
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
的交点N1(1,-6),这个点N1即为所求.
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
),
综上所述,满足条件的点N的坐标为(1,-6)
x=3 y=-2 x=3 x=3 x=3y=-2 y=-2 y=-2
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
的交点N1(1,-6),这个点N1即为所求.
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
),
综上所述,满足条件的点N的坐标为(1,-6)
6 x 6 6 6x x x的交点N11(1,-6),这个点N11即为所求.
②当△M22N22H≌△BAK时,四边形ABM22N22是平行四边形,
∴N22H=AK=4,
∴N22的横坐标为-3,
∴N22(-3,2),同理可得N33(4,-
),
综上所述,满足条件的点N的坐标为(1,-6)
3 2 3 3 32 2 2),
综上所述,满足条件的点N的坐标为(1,-6)
∴OD=4,
∵OD=2OC,
∴OC=2,
∴C(2,0),
把C(2,0)代入y=mx+4,得到2m+4=0,
∴m=-2,
∴直线的解析式为y=-2x+4,
当y=6时,6=-2x+4,
∴x=-1,
∴A(-1,6),
∴k=-6,
∴反比例函数的解析式为y=-
| 6 |
| x |
(2)如图,PE∥OC,

∵P(a,b),
∴E(-
| 6 |
| b |
∴PE=a+
| 6 |
| b |
由题意
| 1 |
| 2 |
| 6 |
| b |
∵b=-2a+4 ②
由①②得到
|
∴a=0.
(3)作AK∥x轴,BK∥y轴交AK于K.作N2H⊥直线x=1于H.

由
|
|
|
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
| 6 |
| x |
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
| 3 |
| 2 |
综上所述,满足条件的点N的坐标为(1,-6)
| 6 |
| x |
(2)如图,PE∥OC,

∵P(a,b),
∴E(-
| 6 |
| b |
∴PE=a+
| 6 |
| b |
由题意
| 1 |
| 2 |
| 6 |
| b |
∵b=-2a+4 ②
由①②得到
|
∴a=0.
(3)作AK∥x轴,BK∥y轴交AK于K.作N2H⊥直线x=1于H.

由
|
|
|
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
| 6 |
| x |
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
| 3 |
| 2 |
综上所述,满足条件的点N的坐标为(1,-6)
| 6 |
| b |
∴PE=a+
| 6 |
| b |
由题意
| 1 |
| 2 |
| 6 |
| b |
∵b=-2a+4 ②
由①②得到
|
∴a=0.
(3)作AK∥x轴,BK∥y轴交AK于K.作N2H⊥直线x=1于H.

由
|
|
|
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
| 6 |
| x |
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
| 3 |
| 2 |
综上所述,满足条件的点N的坐标为(1,-6)
| 6 |
| b |
由题意
| 1 |
| 2 |
| 6 |
| b |
∵b=-2a+4 ②
由①②得到
|
∴a=0.
(3)作AK∥x轴,BK∥y轴交AK于K.作N2H⊥直线x=1于H.

由
|
|
|
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
| 6 |
| x |
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
| 3 |
| 2 |
综上所述,满足条件的点N的坐标为(1,-6)
| 1 |
| 2 |
| 6 |
| b |
∵b=-2a+4 ②
由①②得到
|
∴a=0.
(3)作AK∥x轴,BK∥y轴交AK于K.作N2H⊥直线x=1于H.

由
|
|
|
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
| 6 |
| x |
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
| 3 |
| 2 |
综上所述,满足条件的点N的坐标为(1,-6)
| 6 |
| b |
∵b=-2a+4 ②
由①②得到
|
∴a=0.
(3)作AK∥x轴,BK∥y轴交AK于K.作N2H⊥直线x=1于H.

由
|
|
|
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
| 6 |
| x |
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
| 3 |
| 2 |
综上所述,满足条件的点N的坐标为(1,-6)
|
| a=0 |
| b=4 |
| a=0 |
| b=4 |
| a=0 |
| b=4 |
| a=0 |
| b=4 |
∴a=0.
(3)作AK∥x轴,BK∥y轴交AK于K.作N22H⊥直线x=1于H.

由
|
|
|
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
| 6 |
| x |
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
| 3 |
| 2 |
综上所述,满足条件的点N的坐标为(1,-6)
|
y=-
| ||
| y=-2x+4 |
y=-
| ||
| y=-2x+4 |
y=-
| ||
| y=-2x+4 |
y=-
| ||
| y=-2x+4 |
| 6 |
| x |
| 6 |
| x |
| 6 |
| x |
| 6 |
| x |
|
|
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
| 6 |
| x |
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
| 3 |
| 2 |
综上所述,满足条件的点N的坐标为(1,-6)
|
| x=-1 |
| y=4 |
| x=-1 |
| y=4 |
| x=-1 |
| y=4 |
| x=-1 |
| y=4 |
|
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
| 6 |
| x |
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
| 3 |
| 2 |
综上所述,满足条件的点N的坐标为(1,-6)
|
| x=3 |
| y=-2 |
| x=3 |
| y=-2 |
| x=3 |
| y=-2 |
| x=3 |
| y=-2 |
∴B(3,-2),
∴线段AB被直线x=1平分,
①直线x=1与y=-
| 6 |
| x |
②当△M2N2H≌△BAK时,四边形ABM2N2是平行四边形,
∴N2H=AK=4,
∴N2的横坐标为-3,
∴N2(-3,2),同理可得N3(4,-
| 3 |
| 2 |
综上所述,满足条件的点N的坐标为(1,-6)
| 6 |
| x |
②当△M22N22H≌△BAK时,四边形ABM22N22是平行四边形,
∴N22H=AK=4,
∴N22的横坐标为-3,
∴N22(-3,2),同理可得N33(4,-
| 3 |
| 2 |
综上所述,满足条件的点N的坐标为(1,-6)
| 3 |
| 2 |
综上所述,满足条件的点N的坐标为(1,-6)
看了 已知直线y=mx+4与反比例...的网友还看了以下:
比值是5的比例和比值是0.4的比例各写2个 2020-05-20 …
480比上0.4的比值是多少 2020-06-13 …
480:0.4的比值怎么求, 2020-06-13 …
平面直角坐标系中,有这么些点,坐标分别为(1,0)(2,0)(2,1)(3,2)(3,1)(3,0 2020-06-14 …
已知直线y=-2x+4与x轴,y轴分别相交与A(-2,0)、C(0,4).抛物线y=-1/2X的平 2020-06-14 …
0.4吨比350千克的值是多少? 2020-07-14 …
甲、乙两个乒乓球运动员进行乒乓球单打比赛,已知每一局甲获胜的概率为0.6,乙为0.4.若比赛可采用 2020-07-16 …
2:0.4的比值是,最简整数比是. 2020-07-24 …
列出比例并解比例.1.x和0.4的比等于3.2和1.8的比.2.比例的两个外项分别是4和10,两个 2020-08-02 …
直角坐标系上依次有这样的点:(1,0)(2,0)(2,1)(3,2)(3,1)(3,0)(4,0)( 2020-12-25 …