早教吧作业答案频道 -->数学-->
如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE.(1)求证:△AOE≌△COF;(2)若EF⊥AC,试判断四边形AFCE是什么特殊四边形?请证明
题目详情
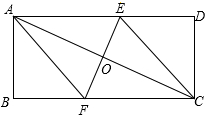
如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE.
(1)求证:△AOE≌△COF;
(2)若EF⊥AC,试判断四边形AFCE是什么特殊四边形?请证明你的结论.如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE.

(1)求证:△AOE≌△COF;
(2)若EF⊥AC,试判断四边形AFCE是什么特殊四边形?请证明你的结论.


(1)求证:△AOE≌△COF;
(2)若EF⊥AC,试判断四边形AFCE是什么特殊四边形?请证明你的结论.如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE.

(1)求证:△AOE≌△COF;
(2)若EF⊥AC,试判断四边形AFCE是什么特殊四边形?请证明你的结论.

▼优质解答
答案和解析
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,
∵O是AC的中点,
∴AO=CO,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA);
(2) 四边形AFCE是菱形;理由如下:
理由是:由(1)△AOE≌△COF得:OE=OF
又∵OA=OC,
∴四边形AFCE是平行四边形,
又∵EF⊥AC
∴平行四边形AFCE是菱形.
∠EAO=∠FCO AO=CO ∠AOE=∠COF ∠EAO=∠FCO ∠EAO=∠FCO ∠EAO=∠FCO AO=CO AO=CO AO=CO ∠AOE=∠COF ∠AOE=∠COF ∠AOE=∠COF
∴△AOE≌△COF(ASA);
(2) 四边形AFCE是菱形;理由如下:
理由是:由(1)△AOE≌△COF得:OE=OF
又∵OA=OC,
∴四边形AFCE是平行四边形,
又∵EF⊥AC
∴平行四边形AFCE是菱形.
∴AD∥BC,
∴∠EAO=∠FCO,
∵O是AC的中点,
∴AO=CO,
在△AOE和△COF中,
|
∴△AOE≌△COF(ASA);
(2) 四边形AFCE是菱形;理由如下:
理由是:由(1)△AOE≌△COF得:OE=OF
又∵OA=OC,
∴四边形AFCE是平行四边形,
又∵EF⊥AC
∴平行四边形AFCE是菱形.
|
| ∠EAO=∠FCO | |
| AO=CO | |
| ∠AOE=∠COF |
| ∠EAO=∠FCO | |
| AO=CO | |
| ∠AOE=∠COF |
| ∠EAO=∠FCO | |
| AO=CO | |
| ∠AOE=∠COF |
| ∠EAO=∠FCO | |
| AO=CO | |
| ∠AOE=∠COF |
∴△AOE≌△COF(ASA);
(2) 四边形AFCE是菱形;理由如下:
理由是:由(1)△AOE≌△COF得:OE=OF
又∵OA=OC,
∴四边形AFCE是平行四边形,
又∵EF⊥AC
∴平行四边形AFCE是菱形.
看了 如图,已知AC是矩形ABCD...的网友还看了以下:
设a=(√5-1)/2,求(a^5+a^4-2a^3-a^2-a+2)/a^3-a∵2a=√5-1 2020-04-05 …
请你观察图形,依据图形面积之间的关系,不需要连其他的线,便可得到一个你非常熟悉的公式,这个公式是( 2020-04-09 …
请教三道高中英语单选题啦~~麻烦进来看看~~1.Amoderncityhasbeensetupwa 2020-04-26 …
(m0h4•黔西南州)&nhsp;如图是A、h、C三种固体物质的溶解度曲线,请回答.(h)th℃时 2020-05-15 …
若关于x的一元二次方程ax²+2x-5=0的两根中有且仅有一根在0和1之间(不含0和1),则a的取 2020-05-15 …
He tried his best to solve the problem,______ dif 2020-05-17 …
下列变形错误的是.a.若a=b,则a-3=b-3b.若a=b,则7a-1=7b-1c.若a=b,则 2020-06-06 …
三国杀中当前回合角色死亡后,属于谁的回合比如三名角色按逆时针顺序是A,张角,和装着八卦的司马懿。A 2020-06-09 …
已知点A,直线a,平面α,以下表达正确的个数是①A∈a,a不包含于α→A真包含于α②A∈,a∈α→ 2020-06-12 …
求证“非非A-->(B-->A)”只是用公理和分离法则,公理如下:(1)A-->(B-->A)(2 2020-06-12 …