我们已经学过了等差数列你是否想到过有没有等和数列呢?(1)类比“等差数列”给出“等和数列”的定义.(2)探索等和数列{an}的奇数项与偶数项各有什么特点并加以说明.

Question

我们已经学过了等差数列 你是否想到过有没有等和数列呢?

(1)类比“等差数列”给出“等和数列”的定义.

(2)探索等和数列{ a _n }的奇数项与偶数项各有什么特点 并加以说明.

(3)在等和数列{ a _n }中 如果 a ₁ = a a ₂ = b 求它的前 n 项和 S _n .

我们已经学过了等差数列 你是否想到过有没有等和数列呢?

(1)类比“等差数列”给出“等和数列”的定义.

(2)探索等和数列{ a _n }的奇数项与偶数项各有什么特点 并加以说明.

(3)在等和数列{ a _n }中 如果 a ₁ = a a ₂ = b 求它的前 n 项和 S _n .

(1)类比“等差数列”给出“等和数列”的定义.

(2)探索等和数列{ a _n }的奇数项与偶数项各有什么特点 并加以说明.

a _{n n}

(3)在等和数列{ a _n }中 如果 a ₁ = a a ₂ = b 求它的前 n 项和 S _n .

a _{n n} a ₁ a a ₂ b n S _{n n}

Answer 1

解:(1)如果一个数列从第2项起 每一项与它的前一项的和等于同一个常数 那么这个数列就叫做等和数列.

(2)由(1)知 a _n + a _{n +1} = a _{n +1} + a _{n +2} .

∴ a _{n +2} = a _n .

∴等和数列的奇数项相等 偶数项也相等.

(3)当 n 为奇数时 令 n =2 K -1 K ∈ N ^* 则 S _n = S _{2 K -1} = S _{2 K -2} + a _{2 K -1} = ( a + b )+ a = ( a + b )+ a = a + b 

当 n 为偶数时 令 n =2 K K ∈ N ^* 则

S _n = S _{2 K} = K ( a + b )= ( a + b ).

∴它的前 n 项和 S _n =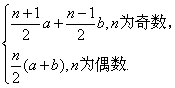

点评:本题是一道浅显的定义类比应用问题 通过对等差数列定义及性质的理解 类比出等和数列的定义和性质 很好地考查同学们类比应用的能力.

解:(1)如果一个数列从第2项起 每一项与它的前一项的和等于同一个常数 那么这个数列就叫做等和数列.

解:(1)如果一个数列从第2项起 每一项与它的前一项的和等于同一个常数 那么这个数列就叫做等和数列.

(2)由(1)知 a _n + a _{n +1} = a _{n +1} + a _{n +2} .

(2)由(1)知 a _n a _n n + a _n a _n n ₊₁ +1 = a _n a _n n ₊₁ +1 + a _n a _n n ₊₂ +2 .

∴ a _{n +2} = a _n .

∴ a _n a _n n ₊₂ +2 = a _n a _n n .

∴等和数列的奇数项相等 偶数项也相等.

∴等和数列的奇数项相等 偶数项也相等.

(3)当 n 为奇数时 令 n =2 K -1 K ∈ N ^* 则 S _n = S _{2 K -1} = S _{2 K -2} + a _{2 K -1} = ( a + b )+ a = ( a + b )+ a = a + b 

(3)当 n n 为奇数时 令 n n =2 K K -1 K K ∈ N N ^* * 则 S _n S _n n = S S _{2 K -1} 2 K K -1 = S S _{2 K -2} 2 K K -2 + a a _{2 K -1} 2 K K -1 = ( a a + b b )+ a a = ( a a + b b )+ a a = a a + b b 

当 n 为偶数时 令 n =2 K K ∈ N ^* 则

当 n n 为偶数时 令 n n =2 K K K K ∈ N N ^* * 则

S _n = S _{2 K} = K ( a + b )= ( a + b ).

S _n S _n n = S S _{2 K} 2 K K = K K ( a a + b b )= ( a a + b b ).

∴它的前 n 项和 S _n =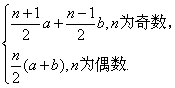

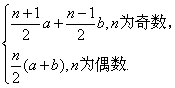
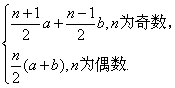
∴它的前 n n 项和 S _n S _n n =

点评:本题是一道浅显的定义类比应用问题 通过对等差数列定义及性质的理解 类比出等和数列的定义和性质 很好地考查同学们类比应用的能力.

点评:本题是一道浅显的定义类比应用问题 通过对等差数列定义及性质的理解 类比出等和数列的定义和性质 很好地考查同学们类比应用的能力.