如图，在三棱锥P-ABC中，AC=BC=2，AP=BP=AB，BC⊥平面PAC．（Ⅰ）求证：PC⊥AB；（Ⅱ）求三棱锥P-ABC的体积．（Ⅲ）（理科做，文科不做）求二面角B-AP-C的正弦值．

Question

如图，在三棱锥P-ABC中，AC=BC=2，AP=BP=AB，BC⊥平面PAC．

（Ⅰ）求证：PC⊥AB；
（Ⅱ）求三棱锥P-ABC的体积．
（Ⅲ）（理科做，文科不做）求二面角B-AP-C的正弦值．

Answer 1

（Ⅰ）证明：取AB中点D，连结PD、CD．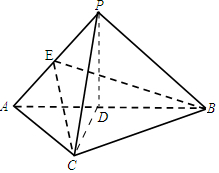
∵AP=BP，∴PD⊥AB．
∵AC=BC，∴CD⊥AB． 
又PD∩CD=D，∴AB⊥平面PCD．
∵PC⊂平面PCD，∴PC⊥AB；
（Ⅱ） ∵BC⊥平面PAC，∴BC⊥AC，BC⊥PC，
又AC=BC=2，∴AB=2√(2)，则AB=AP=PB=2√(2)，
∴PC=2，则PC²+AC²=PA²，即AC⊥PC．
∴S△APC=(1)/(2)×2×2=2，VP-ABC=VB-APC=(1)/(3)•S△APC•BC=(1)/(3)×2×2=(4)/(3)；
（Ⅲ） 取AP中点E，连结BE，CE．
∵AP=BP，∴BE⊥AP，
∵BC⊥平面PAC，∴BC⊥AP，
又∵BE∩BC=B，∴AP⊥平面BEC，则AP⊥EC．
∴∠BEC是二面角B-AP-C的平面角．
∵BC⊥平面PAC，∴BC⊥AC，
又∵AC=BC=2，∴AB=2√(2)，
∵AP=BP=AB，∴BE=(√(3))/(2)AB=√(6)．
∵BC⊥平面PAC，∴BC⊥CE，则∠BCE=90°．
∴在△BCE中，sin∠BEC=(BC)/(BE)=(√(6))/(3)．
故二面角B-AP-C的正弦值为(√(6))/(3)．