早教吧作业答案频道 -->数学-->
如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=26.(1)求证:A′C⊥EF;(2)求五棱锥A′-BCDFE的体积.
题目详情
如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2
.
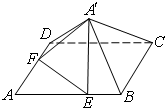
(1)求证:A′C⊥EF;
(2)求五棱锥A′-BCDFE的体积.
| 6 |

(1)求证:A′C⊥EF;
(2)求五棱锥A′-BCDFE的体积.
▼优质解答
答案和解析
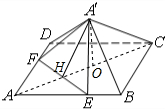 (1)证明:连接AC,设AC∩EF=H,连接A′H,则EF⊥AC,EF⊥A′H,
(1)证明:连接AC,设AC∩EF=H,连接A′H,则EF⊥AC,EF⊥A′H,
∵AC∩A′H=H,
∴EF⊥平面A′HC,
∵A′C⊂平面A′HC,
∴A′C⊥EF;
(2) 由ABCD是正方形,AE=AF=4,
得H是EF的中点,
且EF⊥AH,EF⊥CH,
从而有A′H⊥EF,CH⊥EF,
∴EF⊥平面A′HC,
从而平面A′HC⊥平面ABCD,
过点A′作A′O垂直HC且与HC相交于点O,
则A′O⊥平面ABCD.
∵正方形ABCD的边长为6,AE=AF=4,
得到:A′H=2
,CH=4
,
∴cos∠A′HC=
=
,
∴HO=A′Hcos∠A′HC=
,A′O=
,
∴五棱锥A′-BCDFE的体积V=
×(62-
×4×4)×
=
.
 (1)证明:连接AC,设AC∩EF=H,连接A′H,则EF⊥AC,EF⊥A′H,
(1)证明:连接AC,设AC∩EF=H,连接A′H,则EF⊥AC,EF⊥A′H,∵AC∩A′H=H,
∴EF⊥平面A′HC,
∵A′C⊂平面A′HC,
∴A′C⊥EF;
(2) 由ABCD是正方形,AE=AF=4,
得H是EF的中点,
且EF⊥AH,EF⊥CH,
从而有A′H⊥EF,CH⊥EF,
∴EF⊥平面A′HC,
从而平面A′HC⊥平面ABCD,
过点A′作A′O垂直HC且与HC相交于点O,
则A′O⊥平面ABCD.
∵正方形ABCD的边长为6,AE=AF=4,
得到:A′H=2
| 2 |
| 2 |
∴cos∠A′HC=
| 8+32-24 | ||||
2×2
|
| 1 |
| 2 |
∴HO=A′Hcos∠A′HC=
| 2 |
| 6 |
∴五棱锥A′-BCDFE的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
| 6 |
28
| ||
| 3 |
看了 如图,已知正方形ABCD的边...的网友还看了以下:
1.a≠0,b≠0,则a/|a|+b/|b|的不同取值的个数为()A.3B.2C.1D.02.若|x 2020-03-31 …
采购员用一张1万元支票去购物.购单价为590元的A种物品若干件,又购单价为670元的B种物品若干件 2020-04-07 …
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
基本不等式超费解130已知a>b>0,求a2+1/(a*b)+1/[a*(a-b)]的最小值.a2 2020-05-13 …
在一定温度下,下列叙述不是可逆反应A(气)+3B(气)2C(气)+2D(固)达到平衡的标志的是(a 2020-05-15 …
设集合A={1,a,b},B={a,a^2,ab}且A=B,求实数A,B的值因为集合需要满足互异性 2020-05-15 …
一种一元强酸HA溶液中加入一元碱MOH反应后,溶液呈中性,下列说法正确的是A.加入的碱过量 B.生 2020-05-16 …
关于元素的相对原子质量计算硼有两种天然同位素(10/5)B、(11/5)B,硼元素的近似相对原子质 2020-05-16 …
质量a的A物质,b的B物质充分反应,生成的c为什么小于等于(a+b)?可以小于吗?A+B----C 2020-05-21 …
要测量海岛上一座山峰A的高度AH,立两根高三丈的标竿BC和DE,两杆相距BD=1000步,B.D. 2020-05-23 …